Trick Question (1 Viewer)

[azureus88]

True or false:

[maths]\int_{0}^{1}\frac{dt}{1+t^n}\leq \int_{0}^{1}\frac{dt}{1+t^{n+1}}[/maths] for n=1,2,3,...

It's false cause they cant be equal right?

 

[lolokay]

i don't think they can be equal

 

[Drongoski]

True or false:

[maths]\int_{0}^{1}\frac{dt}{1+t^n}\leq \int_{0}^{1}\frac{dt}{1+t^{n+1}}[/maths] for n=1,2,3,...

It's false cause they cant be equal right?

Over the closed interval [0,1], both integrands are positive and 1/(1 + t^n) is <= 1/(1 + t^(n+1) ); Therefore the left integral <= the right one; i.e. statement is true.

 

[lolokay]

1/(1+tⁿ) <= 1/(1+tⁿ⁺¹) for 0 <= t <= 1
but the equality only exists when t = 0, 1
as the integral also has all other values in the range, it can't be equal

 

[hermand]

1/(1+tⁿ) <= 1/(1+tⁿ⁺¹) for 0 <= t <= 1
but the equality only exists when t = 0, 1
as the integral also has all other values in the range, it can't be equal

but it doesn't have to be all values are equal, just one possible value needs to be equal for it to satisfy that statement.

 

[azureus88]

but it doesn't have to be all values are equal, just one possible value needs to be equal for it to satisfy that statement.

only t = 0, 1 satifies the inequality 1/(1+t<SUP>n</SUP>) <= 1/(1+t<SUP>n+1</SUP>)

But as the question is asking about the integral (ie. area under the curve from 0 to 1), i dont think any value of n will satisfy the inequality(the one in the question).

 

[Templar]

The integral on the left is less than the right, but the statement is true. 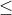means less than or equal to, with the "or" clearly being exclusive or, so there is nothing wrong with that since only one has to be valid ie and are both true.