-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Tricky projectile motion question, Thanks (1 Viewer)
- Thread starter shmitler
- Start date
hmmm, i tried that and still got answer wrong, these were my steps
100t-86.6t=600, therefore t=44.78
then i plugged t=44.78 into y=1/2gt^2+vsinθt +H (with v=100 and θ =30)
since we have the time of flight the value of y will be zero leading to the only unknown being H.
Thanks
What is the given answer and what answer are you getting?hmmm, i tried that and still got answer wrong, these were my steps
100t-86.6t=600, therefore t=44.78
then i plugged t=44.78 into y=1/2gt^2+vsinθt +H (with v=100 and θ =30)
since we have the time of flight the value of y will be zero leading to the only unknown being H.
Thanks
hahahaha really different, answer is 88 m, im getting around -7000What is the given answer and what answer are you getting?
For both balls we have
 &= -\frac{9.8}{2}t^2+100\sin(\pi/6)t+h \\ x_1(t) &=100\cos(\pi/6)t\end{cases})
 &= -\frac{9.8}{2}t^2+h \\ x_2(t) &=100t\end{cases})
Solve = 0) and
and  = 0) to get the time of flight for each ball (call these
to get the time of flight for each ball (call these  and
and  ).
).
Obviously the ball shot straight horizontally will hit the ground sooner (and will travel less), so you need to solve
-x_2(t_2) = 600) (not the other way around!)
(not the other way around!)
for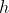 .
.
I calculated .
.
Solve
Obviously the ball shot straight horizontally will hit the ground sooner (and will travel less), so you need to solve
for
I calculated
Last edited:

