Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Trig Help (1 Viewer)
- Thread starter Lith_30
- Start date
-
- Tags
- math homework
username_2
Active Member
- Joined
- Aug 1, 2020
- Messages
- 116
- Gender
- Male
- HSC
- 2020
Well uh have you tried auxiliary angle method where you let: R sin(x + a) = cos(x) + 3sin(x)How would is solve a question like this.
View attachment 33616
R = sqrt(3^2+1^2) = sqrt(10)
a = cos^-1(1/sqrt(10)) = 1.249
Hence, you can solve the equation:
sqrt(10) sin(x+1.249) = 1
And i trust you can do it from here.
The first approaches that come to mind for me here are T formulae and aux angle but those approaches are out of question as this was posted in the Advanced forum.
Square both sides of the equation and use the Pythagorean identity to get a quadratic in terms of sine or cosine. Solve said quadratic as normal, but be sure to disregard any solutions that are outside the range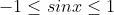 or
or 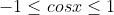 . Also pay attention to the given domain, and substitute the values into the original equation to see if it matches up (squaring an equation provides extra solutions).
. Also pay attention to the given domain, and substitute the values into the original equation to see if it matches up (squaring an equation provides extra solutions).
Square both sides of the equation and use the Pythagorean identity to get a quadratic in terms of sine or cosine. Solve said quadratic as normal, but be sure to disregard any solutions that are outside the range
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
How would is solve a question like this.
View attachment 33616
Um, do Mathematics Advanced students learn the Auxillary angle method? Did this come from an Extension I textbook?Well uh have you tried auxiliary angle method where you let: R sin(x + a) = cos(x) + 3sin(x)
R = sqrt(3^2+1^2) = sqrt(10)
a = cos^-1(1/sqrt(10)) = 1.249
Hence, you can solve the equation:
sqrt(10) sin(x+1.249) = 1
And i trust you can do it from here.
Actually I have a way out of this square both sides in doing so we have
Last edited:
okayokay123
Member
- Joined
- Aug 8, 2020
- Messages
- 34
- Gender
- Female
- HSC
- 2021
This is an Extension 1 question not an Advanced question. you would have to used auxillary method, t formulae etc.
I have heard about the auxiliary method but I haven't learnt it. Also, thankyou!Well uh have you tried auxiliary angle method where you let: R sin(x + a) = cos(x) + 3sin(x)
R = sqrt(3^2+1^2) = sqrt(10)
a = cos^-1(1/sqrt(10)) = 1.249
Hence, you can solve the equation:
sqrt(10) sin(x+1.249) = 1
And i trust you can do it from here.
Not really sure, this was just part of the homework given to me by my advanced teacher. I probably will ask her were she got this.Did this come from an Extension I textbook?
ExtremelyBoredUser
Bored Uni Student
The only way I can think of inside the syllabus is by graphing the function and finding the values by just finding the points that are at 1.I have heard about the auxiliary method but I haven't learnt it. Also, thankyou!
Not really sure, this was just part of the homework given to me by my advanced teacher. I probably will ask her were she got this.
The question in your original post is Question 7A of Exercise 12.2 ["Further Solution of Trigonometric Equations"] from the New Senior Mathematics Advanced textbook. Example 10 from the same exercise tackles a similar style question:Not really sure, this was just part of the homework given to me by my advanced teacher. I probably will ask her were she got this.

specificagent1
Well-Known Member
- Joined
- Aug 24, 2021
- Messages
- 1,968
- Gender
- Male
- HSC
- 2021
this does not look like advance lol
Squaring then testing the resulting solutions (to exclude "solutions" created by the squaring) is an accepted Advanced method. The auxiliary angle method is the standard method for such equations but is not taught below MX1 level.


