HOLY SHIT WHAT IS THIS EPIPHANY OMFGn=2,, which is divisible by
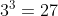
Nuuuuuuuuuuuuuuuu wow I should've just wrote k=n+1
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HOLY SHIT WHAT IS THIS EPIPHANY OMFGn=2,, which is divisible by
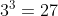
bad luck!HOLY SHIT WHAT IS THIS EPIPHANY OMFG
Nuuuuuuuuuuuuuuuu wow I should've just wrote k=n+1
My approach:bad luck!anyways what i really wanna know is how you can actually prove this. Realise, i was also trying an induction in the last 5 minutes but to no avail.
Yep yep same here. I tried messing around with stuff like letting x=3^n but yeah, that didnt work out... was running out of time so just wrote down what i had observed from the results from the first few cases.My approach:
Prove that:
Where 'p' is not divisible by 3.
Then factorise and equate, something along the lines of that. I had fricking n+1 the whole time and I kept stumbling with the "k=2 when n=2"Yep yep same here. I tried messing around with stuff like letting x=3^n but yeah, that didnt work out... was running out of time so just wrote down what i had observed from the results from the first few cases.
Everyone who did it seems to have found this question challenging.
}$ Suppose that $x_{1},x_{2},x_{3}$ and $y_{1},y_{2},y_{3}$ are positive real numbers such that$\\\\0< x_{1}y_{1}<x_{2}y_{2}<x_{3}y_{3}\\\\$and$\\\\x_{1}+x_{2}+x_{3}\geq y_{1}+y_{2}+y_{3}.\\\\$Prove that$\\\\\frac{1}{x_{1}}+\frac{1}{x_{2}}+\frac{1}{x_{3}}\leq \frac{1}{y_{1}}+\frac{1}{y_{2}}+\frac{1}{y_{3}}.)
1) Prove that 'n' has to be a multiple of 2 (fairly straight forward and obvious as you need an even amount of terms so that all 1's and -1's cancel out).Realise how did you do Q5?
alright well i was messing around with cases and wrote something along those lines. someone who did it was saying something about factoring out terms and then summing them.1) Prove that 'n' has to be a multiple of 2 (fairly straight forward and obvious as you need an even amount of terms so that all 1's and -1's cancel out).
2)Prove that 'n' can be a multiple of 4. This is done by considering 4 terms:
Now this will always sum to 0 if only one of the x's is -1, and the other 3 are 1. So it is possible for 'n' to be a multiple of 4 by applying this method to all groups of 4.
3) Prove that 'n' can't be a multiple of 2 that isn't a multiple of 4, i.e.
Well you know the firstterms will sum to 0, so you prove the last 2 terms can never equal 0, etc.
