Arrowshaft
Well-Known Member
Hey there, was wondering if we are allowed to use 4U techniques such as implicit differentiation to 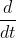 both sides of an equation for related rates as its so much easier than using chain rule. If we cannot, is there an assortment of techniques we can use from 4U is there simply no techniques we can administer to achieve full marks on a question. Thanks.
both sides of an equation for related rates as its so much easier than using chain rule. If we cannot, is there an assortment of techniques we can use from 4U is there simply no techniques we can administer to achieve full marks on a question. Thanks.
