seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
The fundamental theorem of algebra asserts that any non-constant polynomial with complex coefficients has a complex root.
It is notorious as being quite hard to prove for what it is, typically requiring some machinery at least as advanced as complex analysis / vector calculus / algebraic topology.
The most MX2 level proof I know of isn't too advanced, and I have posted it here before as a question (*). However, it is rather unenlightening in nature.
Here is a different "proof" that is easy to visualise and explain to students.
Take
=\sum_{k=0}^n a_kz^k.)
We might as well assume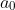 is nonzero, otherwise the problem is trivial.
is nonzero, otherwise the problem is trivial.
Consider the curves:
=\{p(r\textrm{cis}(\theta)):\theta\in [0,2\pi)\}.)
Recall that the highest degree terms and lowest degree terms of a polynomial dominate its behaviour at large and small inputs respectively. (Eg consider the difference between squaring a tiny number and squaring a huge number. In the former case we get much much smaller, and in the latter case we get much much larger.)
This means that for small r, C(r) resembles (with some tiny wobbles from the less relevant terms)
=\{a_0+a_1r\textrm{cis}(\theta):\theta\in[0,2\pi] \})
and for large r, C(r) resembles (with some tiny wobbles from the less relevant terms):
=\{a_nr^n\textrm{cis}(n\theta):\theta\in[0,2\pi] \})
C1 is a small circle around a0
C2 is a big circle around the origin.
Now think about what happens as we increase r.
C(r) expands and gets less circular, but it will always have an inside and an outside (things it wraps around and things it doesn't).
For small r we know the origin is on the outside of C(r) because it is on the outside of C1(r), but for large r we know the origin is on the inside of C(r) because it is on the inside of C2(r).
The only way for this transition to occur is for the curve C(r) to pass through the origin for some r, which implies the existence of a complex root of modulus r!
Note: The idea in this "proof" is perfectly valid, but it is actually quite technical/difficult to make rigorous. Nevertheless I think it is one of the easiest ways to visualise why the theorem should be true!
(*)- The idea was to prove that a polynomial cannot have a local non-zero minimum by direct algebraic manipulation, and then using the extreme value theorem (the only out of syllabus assumption) to show that any polynomial must have a local minimum. Here, a minimum of a polynomial means a minimum of |P(z)|. This remains the least technical proof of the FTA that I know of.
It is notorious as being quite hard to prove for what it is, typically requiring some machinery at least as advanced as complex analysis / vector calculus / algebraic topology.
The most MX2 level proof I know of isn't too advanced, and I have posted it here before as a question (*). However, it is rather unenlightening in nature.
Here is a different "proof" that is easy to visualise and explain to students.
Take
We might as well assume
Consider the curves:
Recall that the highest degree terms and lowest degree terms of a polynomial dominate its behaviour at large and small inputs respectively. (Eg consider the difference between squaring a tiny number and squaring a huge number. In the former case we get much much smaller, and in the latter case we get much much larger.)
This means that for small r, C(r) resembles (with some tiny wobbles from the less relevant terms)
and for large r, C(r) resembles (with some tiny wobbles from the less relevant terms):
C1 is a small circle around a0
C2 is a big circle around the origin.
Now think about what happens as we increase r.
C(r) expands and gets less circular, but it will always have an inside and an outside (things it wraps around and things it doesn't).
For small r we know the origin is on the outside of C(r) because it is on the outside of C1(r), but for large r we know the origin is on the inside of C(r) because it is on the inside of C2(r).
The only way for this transition to occur is for the curve C(r) to pass through the origin for some r, which implies the existence of a complex root of modulus r!
Note: The idea in this "proof" is perfectly valid, but it is actually quite technical/difficult to make rigorous. Nevertheless I think it is one of the easiest ways to visualise why the theorem should be true!
(*)- The idea was to prove that a polynomial cannot have a local non-zero minimum by direct algebraic manipulation, and then using the extreme value theorem (the only out of syllabus assumption) to show that any polynomial must have a local minimum. Here, a minimum of a polynomial means a minimum of |P(z)|. This remains the least technical proof of the FTA that I know of.
