philly2000
New Member
- Joined
- Feb 11, 2009
- Messages
- 29
- Gender
- Male
- HSC
- 2010
Prove 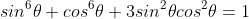
Thanks!
Thanks!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
LHS = (1-cos^2@)^2 (1-cos^2@) + cos^6@ + 3sin^2@cos^2@Prove
Thanks!
nah thats not righti think this way works aswell
sin^6@ + cos^6@ + 3sin^2@cos^2@ = 1
LHS = (sin^2@)^3 + (cos^2@)^3 + 3sin^2@cos^2@
= (sin^2@ + sin^2@)^3 - 3sin^2@cos^2@ + 3sin^2@cos^2@
= (sin^2@ + sin^2@)^3+0
= (1)^3
=1
RHS
somone1 check plz
i don't know if there is a rule for cubes like sqaures (e.g. (x+y)^2-2xy=x^2+y^2)
but here it is anyway
x^3 + y^3 = (x+y)^3
=x^3 + 2x^y + y^2x + yx^2 + 2xy^2 + y^3 - 3xy
=x^3 + y^3 + 3x^2y + 3y^2x
=x^3 + y^3 = 3xy(x+y)
now letting x = sin^2@
y = cos^2@
the 3xy(x+y) --> 3sin^2@cos^2@(sin^2@+cos^2@)
3sin^2@cos^2@(1)
3sin^2@cos^2@
nah thats not right
sin^6@ + cos^6@ + 3sin^2@cos^2@ = 1
LHS=(sin2@+cos2@)3 -3sin4@cos2@ -3sin2@cos4@+3sin2@cos2@
=1+3sin2@cos2@(1-sin2@-cos2@)
=1+3sin2@cos2@(cos2@-cos2@)
=1=RHS
thats how u wud do it that way.
lol woah, what happenned therewonder if I'm wasting everyone's time by posting another one (or has someone already done one exactly the same way; if so I'm sorry)
\left (sin^{4}\theta -sin^{2}\theta cos^{2}\theta +cos^{4}\theta \right )\ +\ 3sin^{2}\theta cos^{2}\theta \\ \\ =\ \ sin^{4}\theta \ +\ 2sin^{2}\theta cos^{2}\theta \ + \ cos^{4}\theta \\ \\ =\ \ \left (sin^{2}\theta +cos^{2}\theta \right )^{2}\\ \\ =\ \ 1^{2} \ \ =\ \ 1\ \\ \\ =\ \ RHS\\ \\ \\ QED)
elegantwonder if I'm wasting everyone's time by posting another one (or has someone already done one exactly the same way; if so I'm sorry)
\left (sin^{4}\theta -sin^{2}\theta cos^{2}\theta +cos^{4}\theta \right )\ +\ 3sin^{2}\theta cos^{2}\theta \\ \\ =\ \ sin^{4}\theta \ +\ 2sin^{2}\theta cos^{2}\theta \ + \ cos^{4}\theta \\ \\ =\ \ \left (sin^{2}\theta +cos^{2}\theta \right )^{2}\\ \\ =\ \ 1^{2} \ \ =\ \ 1\ \\ \\ =\ \ RHS\\ \\ \\ QED)
pretty smart way i thought.lol woah, what happenned there
lol cant see it hahapretty smart way i thought.
he used cube rule then ye he "worked" it
wot?lol cant see it haha
lol nvm i get itwot?
um..not reallyYea that's the way i did it. But it was a bit messy. And hard to see
nope, ur ways wrong, and u were trying to do it the way i did it.Yea that's the way i did it. But it was a bit messy. And hard to see
you cited the sum of 2 cubes identity wrong; pl see my edited posting.Yea that's the way i did it. But it was a bit messy. And hard to see
as i said before thats wrong,
lol pwnedas i said before thats wrong,
u just worked from the answer to get that lol
(sin2@+cos2@)3 =/= sin6@+cos6@+3sin2@cos2@
