K4M1N3
Member
- Joined
- Jun 7, 2010
- Messages
- 177
- Gender
- Male
- HSC
- 2011
Q. The Polynomial equation P(x) = 0 has a double root at x = a. By writing:
=(x-a)^2.Q(x)) Where Q(x) is a polynomial
Where Q(x) is a polynomial
Show that P'(a) = 0
I was just wondering since P(x) has only a double root at x = a......Doesn't that mean that the polynomial Q(x) does NOT have a root at x = a?
i.e.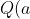\neq 0)
Show that P'(a) = 0
I was just wondering since P(x) has only a double root at x = a......Doesn't that mean that the polynomial Q(x) does NOT have a root at x = a?
i.e.
