-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Maths problem.. (1 Viewer)
- Thread starter epicFAILx
- Start date
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Firstly! Find the point of intersection.


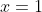
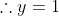
Point of intersection is) .
.
Now this question is rather an odd one, usually we would find the gradient then use the 2 points formula. However in this case, we can inspect what the equation is. The reason we cannot use the gradient formula is because the denominator will be equal to zero. (which is undefined)
Plot) and
and ) on your graph. Draw a straight line through both, you will see the equation of the straight line is
on your graph. Draw a straight line through both, you will see the equation of the straight line is 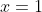
Point of intersection is
Now this question is rather an odd one, usually we would find the gradient then use the 2 points formula. However in this case, we can inspect what the equation is. The reason we cannot use the gradient formula is because the denominator will be equal to zero. (which is undefined)
Plot
..actually.. how come the y was changed too x??Oh! Now i understand..wait a sec
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
No worries.Oh! Now i understand. Thankyou
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
You gave me two equations,..actually.. how come the y was changed too x??
See how they are both equal to
If they are both equal to
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
All the best with your questions.OH. Right... Haha.
THanks
This happens to be a simple case. In general if L1 = 0 and L2 = 0 are equations of the 2 intersecting lines in General Form, then any line thru their intersection is of form: L1 + kL2 = 0 for some constant k.
Here the general form of line thru their intersection is: (x+y-2) + k(x-2) = 0
Since (1,-2) lies on this line: (1-2-2) + k(1+2) = 0 ==> k = 1
.: (x+y-2) + 1(x-y ) = 0
i.e. x = 1
In general this method is easier. Perversely, it seems harder for this question.
Here the general form of line thru their intersection is: (x+y-2) + k(x-2) = 0
Since (1,-2) lies on this line: (1-2-2) + k(1+2) = 0 ==> k = 1
.: (x+y-2) + 1(x-y ) = 0
i.e. x = 1
In general this method is easier. Perversely, it seems harder for this question.
Last edited:
This guy speaks the truth.This happens to be a simple case. In general if L1 = 0 and L2 = 0 are equations of the 2 intersecting lines in General Form, then any line thru their intersection is of form: L1 + kL2 = 0 for some constant k.
Here the general form of line thru their intersection is: (x+y-2) + k(x-2) = 0
Since (1,-2) lies on this line: (1-2-2) + k(1+2) = 0 ==> k = 1
.: (x+y-2) + 1(x-y ) = 0
i.e. x = 1
In general this method is easier. Perversely, it seems harder for this question.
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 848
- Gender
- Male
- HSC
- 2010
nice, but the HSC doesn't test this as often , which they should since it's in the syllabus AND taught at schoolThis happens to be a simple case. In general if L1 = 0 and L2 = 0 are equations of the 2 intersecting lines in General Form, then any line thru their intersection is of form: L1 + kL2 = 0 for some constant k.
Here the general form of line thru their intersection is: (x+y-2) + k(x-2) = 0
Since (1,-2) lies on this line: (1-2-2) + k(1+2) = 0 ==> k = 1
.: (x+y-2) + 1(x-y ) = 0
i.e. x = 1
In general this method is easier. Perversely, it seems harder for this question.
