-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Hellooooooo fellow 4 uniter's (1 Viewer)
- Thread starter b3kh1t
- Start date
lol how when that will give you a real value hahaha
umad?
well Mirakon what you reckon??
mirakon
nigga
- Joined
- Sep 18, 2009
- Messages
- 4,221
- Gender
- Male
- HSC
- 2011
? if you have n=2 then it becomes e^(-pi) which I'm pretty sure is not equal to i^i (correct me if I am wrong)Umm....
where n is a positive odd integer
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Essentially, you need to know Euler's Identity to solve this.lol how when that will give you a real value hahaha
well Mirakon what you reckon??
e^(i.pi) + 1 = 0
e^(i.pi) = -1
e^(i.pi/2) = i (square root)
e^(-pi/2) = i^i (raise to the i; i*i = -1)
K4M1N3
Member
- Joined
- Jun 7, 2010
- Messages
- 177
- Gender
- Male
- HSC
- 2011
buddy learn to read, n has a restriction for odd integers only!? if you have n=2 then it becomes e^(-pi) which I'm pretty sure is not equal to i^i (correct me if I am wrong)
aiight but in the last line how did you get thatEssentially, you need to know Euler's Identity to solve this.
e^(i.pi) + 1 = 0
e^(i.pi) = -1
e^(i.pi/2) = i (square root)
e^(-pi/2) = i^i (raise to the i; i*i = -1)
cheese_cheese
Member
- Joined
- Oct 20, 2011
- Messages
- 403
- Gender
- Male
- HSC
- 2006
This guy knows his complex numbers.Umm....
where n is a positive odd integer
K4M1N3
Member
- Joined
- Jun 7, 2010
- Messages
- 177
- Gender
- Male
- HSC
- 2011
Do i detect sarcasm?This guy knows his complex numbers.
aiight cool but where does the e come from or is this a rule??
It is basically just the usual index laws combined with the fact that:
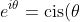)
cheese_cheese
Member
- Joined
- Oct 20, 2011
- Messages
- 403
- Gender
- Male
- HSC
- 2006
No, I was giving you a compliment.Do i detect sarcasm?
cheese_cheese
Member
- Joined
- Oct 20, 2011
- Messages
- 403
- Gender
- Male
- HSC
- 2006
You'd cover it in most first year algebra courses at uni. Don't think it is 4U though.i do not think Euler's Identity is syllabus, but if you do a bit of extra-curricular maths you may know it
