Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Integration volume question (1 Viewer)
- Thread starter nazfiz
- Start date
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
y=9-x^2
a) V=pi*integral[(9-x^2)^2] dx from x=0 to x=3
V=pi*integral[81-18x^2+x^4] dx from x=0 to x=3
V=pi[81x-6x^3+(1/5)x^5] from x=0 to x=3
V=648pi/5 u^3
b) x^2=9-y
V=pi*integral[9-y] dy from y=0 to y=9
V=pi[9y-(1/2)y^2] from y=0 to y=9
V=pi[9*9-(1/2)*9^2]=81pi/2 u^3
sorry for the confusion, i have edited
a) V=pi*integral[(9-x^2)^2] dx from x=0 to x=3
V=pi*integral[81-18x^2+x^4] dx from x=0 to x=3
V=pi[81x-6x^3+(1/5)x^5] from x=0 to x=3
V=648pi/5 u^3
b) x^2=9-y
V=pi*integral[9-y] dy from y=0 to y=9
V=pi[9y-(1/2)y^2] from y=0 to y=9
V=pi[9*9-(1/2)*9^2]=81pi/2 u^3
sorry for the confusion, i have edited
Last edited:
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
no worries dude, btw ur in year 10, y r u asking this? (u can call me a hyprocrite i guess for saying as i am in year 10 too answering it lol)
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
I see you're working pretty far ahead.
First, draw a graph so you know what you're working with.

a) Volume of shaded region rotated about x axis is given by:
^2 dx)


 )

b)
Volume of shaded area rotated around the y-axis is given by:


)

First, draw a graph so you know what you're working with.

a) Volume of shaded region rotated about x axis is given by:
b)
Volume of shaded area rotated around the y-axis is given by:
Last edited:
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
disregard my answer to the first one, i ended up integrating [9-x^2] not [9-x^2]^2 lol, i need to learn latex much clearer...
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
nightweaver, u didnt realise the area to be rotated was bounded by the curve and the ordinate axis ie the x and y axis
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Misread the question lol. Will edit my post a bit.nightweaver, u didnt realise the area to be rotated was bounded by the curve and the ordinate axis ie the x and y axis
Thanks guys
LOL, a majority of my school grade knows this stuff. I guess after the SC everyone tends to work a little ahead.no worries dude, btw ur in year 10, y r u asking this? (u can call me a hyprocrite i guess for saying as i am in year 10 too answering it lol)
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
u must go to a gun school if so lol
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
lol
Pfortune35
Member
- Joined
- Apr 25, 2011
- Messages
- 270
- Gender
- Male
- HSC
- 2013
solution to roation around x axis given above is correct
for y axis
having tech diffuculties
for y axis
having tech diffuculties
hey guys, I've got another question. sorry to be a pain.
A drinking glass has the shape of a truncated cone. If the internal radii of the base and the top are 3cm and 4 cm respectively and the depth is 10cm, find by integration, its capacity. If the glass is filled with water to a depth of 5cm, find the volume of the water.
A drinking glass has the shape of a truncated cone. If the internal radii of the base and the top are 3cm and 4 cm respectively and the depth is 10cm, find by integration, its capacity. If the glass is filled with water to a depth of 5cm, find the volume of the water.
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
dude, im pretty sure that is 4 unit maths, but i did it anywayz. i got 127pi/3 cm^3 for the volume, hence the capacity is 127pi/3 mL. where did this question come from?
Last edited:
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
i used 4U lol
sick_kent
Member
- Joined
- May 4, 2011
- Messages
- 71
- Gender
- Male
- HSC
- 2013
To do it with Integration;hey guys, I've got another question. sorry to be a pain.
A drinking glass has the shape of a truncated cone. If the internal radii of the base and the top are 3cm and 4 cm respectively and the depth is 10cm, find by integration, its capacity. If the glass is filled with water to a depth of 5cm, find the volume of the water.
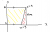
Would you not Intergrate;(Yellow Area+Red Area being A1, Red Area being A2)
Sorry, fucked up integration bit,
pi (integrand) from 1 to 10 (x=10)^2 -((y - 30)/10 = x)^2
Last edited:
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,502
- Gender
- Male
- HSC
- 2013
^ i lold at this attempt
Last edited:
