HSC 2012 MX2 Marathon (archive) (1 Viewer)

SpiralFlex · Jan 9, 2012

Re: 2012 HSC MX2 Marathon

You are right.

Note: People who have posted in this thread are NOT ALLOWED to answer this. I want some fellow extension 2 students to feel welcomed.

$a) Solve in mod arg form: z^4+1=0$

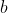$b) Plot the roots on an Argand diagram.$

$c) Find the area of the quadrilateral formed by these roots.$

Trebla · Jan 9, 2012

Re: 2012 HSC MX2 Marathon

largarithmic said:
$$(ii) In the case when n is odd, \textbf{\underline{shower}} by considering $(\sqrt{a+1} + \sqrt{a})T_m$ where m is even, or otherwise, that Tn can be written in the form $C_n\sqrt{a+1} + D_n \sqrt{a}$ where Cn and Dn are integers depending on a and n and $(a+1)C_n^2 = aD_n^2 + 1$

lol

deswa1 · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

$a) z^4&=-1$
$&=cis(\pi +2k\pi)$
$&=cis(\pi/4), cis(3\pi/4), cis(-\pi/4), cis(-3\pi/4)$

I don't know how to plot them on here but the third part:
c) All diagonals are equal length (all have modulus 1). They are perpendicular to each other (separation of pi degrees). Therefore the quadrilateral is a square with diagonal length 2 units. Each side has length root 2 so the area of the quad is 2 units squared.

Hooray, first time using latex

.
A few questions: How do you type text without it becoming bunched up and how do you align your equals signs? I tried following the guide but it wasn't working...

deswa1 · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

Thanks for that

. How would you do this question:

I could do it but the second part took me a bit of time whilst in the answers they just wrote it down with no working (past school paper). Am I missing something ridiculously simple?

Carrotsticks · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

deswa1 said:
Thanks for that . How would you do this question:
View attachment 24089

I could do it but the second part took me a bit of time whilst in the answers they just wrote it down with no working (past school paper). Am I missing something ridiculously simple?

Show us the method that you used.

rawrence · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

deswa1 said:
Thanks for that . How would you do this question:
View attachment 24089

I could do it but the second part took me a bit of time whilst in the answers they just wrote it down with no working (past school paper). Am I missing something ridiculously simple?

Answer the second question using first

deswa1 · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

The answer is pi/4. The way I did it was find the gradient of the line passing through the origin that was a tangent to the parabola since that would have the minimum argument of z and then used the fact that the gradient of a line equals the tangent of the argument to get pi/4. There must be some easier way though isn't there?

lolcakes52 · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

deswa1 said:
The answer is pi/4. The way I did it was find the gradient of the line passing through the origin that was a tangent to the parabola since that would have the minimum argument of z and then used the fact that the gradient of a line equals the tangent of the argument to get pi/4. There must be some easier way though isn't there?

Did you sketch the graph? That sometimes gives the answer away especially in complex number questions. However I don't think there is a quicker algebraic method but I could be wrong.

bleakarcher · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

I considered that the arg(z)=tan^(-1)[y/x] and once I had the cartesian equation of the curve I just used calculus. Note that the curve is a parabola that is concave up and that the minimum clearly must occur in the first quadrant

Carrotsticks · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

The method I'm using below can be handy sometimes, because it gives me max AND min argument immediately. Of course there are other ways, but it's really just preference.:

$\text{The locus is defined to be } y=\frac{1}{4} (x^2+4) \\ \text{The line going through the origin and touching the curve, hence yielding the max/min argument, is in the form: }\\y=mx$

$\text{Substitute into one another to acquire a quadratic in terms of x and m: }\\ x^2-4mx+4=0$

$\text{Let the discriminant be equal to 0, since we are looking for tangents (which have 1 root with the curve) and solve for m:}$

$m=\pm 1\\ \\ \therefore tan\theta =\pm 1 \\ \\ \therefore \theta = \pm \frac{\pi}{4}$

$\text{Thus, minimum argument is } \frac{\pi}{4}$

EDIT:

bleakarcher said:
I considered that the arg(z)=tan^(-1)[y/x] and once I had the cartesian equation of the curve I just used calculus. Note that the curve is a parabola that is concave up and that the minimum clearly must occur in the first quadrant

How did you use calculus for this problem?

bleakarcher · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

arg(z)=tan^(-1)[y/x]=tan^(-1)[(x^2+4)/4x]. Let arg(z)=A.
Now, A=tan^(-1)[(x^2+4)/4x]
Differentiate with respect to x and set the derivative equal to 0 in order to find the point at which A is a minimum. You find that a minimum occurs at the point (2,2). Hence it follows that the minimum value for the arg(z)=tan^(-1)[2/2]=tan^(-1)[1]=pi/4

Carrotsticks · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

bleakarcher said:
arg(z)=tan^(-1)[y/x]=tan^(-1)[(x^2+4)/4x]. Let arg(z)=A.
Now, A=tan^(-1)[(x^2+4)/4x]
Differentiate with respect to x and set the derivative equal to 0 in order to find the point at which A is a minimum. You find that a minimum occurs at the point (2,2). Hence it follows that the minimum value for the arg(z)=tan^(-1)[2/2]=tan^(-1)[1]=pi/4

It's good to see new methods pop up. I never thought of this. Nice work!

However, It is a wee bit slow. Another problem I can see coming is that you will need to actually show that it is in fact max/min, which can get quite tedious.

bleakarcher · Jan 10, 2012

Re: 2012 HSC MX2 Marathon

yeh lol, i couldnt think of anything else.

Carrotsticks · Jan 11, 2012

Re: 2012 HSC MX2 Marathon

bleakarcher said:
yeh lol, i couldnt think of anything else.

Better than being stuck and not thinking at all

bleakarcher · Jan 11, 2012

Re: 2012 HSC MX2 Marathon

true.

deswa1 · Jan 11, 2012

Re: 2012 HSC MX2 Marathon

Thanks guys. The way I did it was Carrotsticks way but I don't get how that can only be a one mark question...

seanieg89 · Jan 11, 2012

Re: 2012 HSC MX2 Marathon

Carrotsticks said:
It's good to see new methods pop up. I never thought of this. Nice work!

However, It is a wee bit slow. Another problem I can see coming is that you will need to actually show that it is in fact max/min, which can get quite tedious.

It can be made pretty fast...observe that arctan is an increasing function of the positive reals and that $x^2+4=(x-2)^2+4x\geq 4x$ with equality attained at x=2.

So
$\arctan(\theta)\geq \arctan(1)\Rightarrow \arg(z)\geq \pi/4.$
with equality attained for some z.

Carrotsticks · Jan 11, 2012

Re: 2012 HSC MX2 Marathon

deswa1 said:
Thanks guys. The way I did it was Carrotsticks way but I don't get how that can only be a one mark question...

If it's only a 1 mark question, then a solution by simple inspection will suffice (seanieg89's way).

If it is more, then perhaps a more 'definite' proof may be required.

maths lover · Jan 11, 2012

Re: 2012 HSC MX2 Marathon

Carrotsticks said:
The method I'm using below can be handy sometimes, because it gives me max AND min argument immediately. Of course there are other ways, but it's really just preference.:

$\text{The locus is defined to be } y=\frac{1}{4} (x^2+4) \\ \text{The line going through the origin and touching the curve, hence yielding the max/min argument, is in the form: }\\y=mx$

$\text{Substitute into one another to acquire a quadratic in terms of x and m: }\\ x^2-4mx+4=0$

$\text{Let the discriminant be equal to 0, since we are looking for tangents (which have 1 root with the curve) and solve for m:}$

$m=\pm 1\\ \\ \therefore tan\theta =\pm 1 \\ \\ \therefore \theta = \pm \frac{\pi}{4}$

$\text{Thus, minimum argument is } \frac{\pi}{4}$

EDIT:

How did you use calculus for this problem?

i am going to rep you for this very intuitive method(me thinks). avoids allot of the tedious trigonometry i usually use for these types of questions.

rolpsy · Jan 12, 2012

Re: 2012 HSC MX2 Marathon

$\\\textup{The exponential function can be defined as: } e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots,\\ \textup{and the sine function as: } \sin (x)= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots.$

$\begin{align*}\textup{(a) } &\textup{Show that:}\\\textit{i. }& \frac{\mathrm{d} }{\mathrm{d} x} \left ( e^x \right ) = e^x\\\textit{ii. }& \cos (x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \\\textup{(b) } &\textup{Show:}\\&e^{i \theta} = \cos (\theta) + i \sin(\theta)\\\textup{(c) } &\textup{Prove:}\\\textit{i. }& \cos(x) = \frac{e^{ix} + e^{-ix}}{2}\\\textit{ii. }& \sin(x) = \frac{e^{ix} - e^{-ix}}{2i}\end{align*}$

Make a Difference – Donate to Bored of Studies!

HSC 2012 MX2 Marathon (archive) (1 Viewer)

Well-Known Member

Administrator

Well-Known Member

Well-Known Member

Retired

Member

Well-Known Member

Member

Active Member

Retired

Active Member

Retired

Active Member

Retired

Active Member

Well-Known Member

Well-Known Member

Retired

Member

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)