Re: 2012 HSC MX2 Marathon
Not really something that would appear in the HSC (perhaps a trial if some school likes weird questions).
Consider a unit circle. Inscribed within this unit circle is an equilateral triangle such that all 3 vertices touch the circle. Inscribed within this triangle is another circle such that all 3 sides of the triangle are in contact with the circle.
This process repeats infinitely.
Find the limiting ratio Red : Green as the number of iterations approaches infinity.
cool problem!!!
Anyway here's how I'd do it.
Observation: each circle has half the radius as the one before it.
Proof: Clearly all the circles, since the diagram has rotational symmetry, have the same centre; call this O. Now let a vertex of say the biggest triangle by A, and the second biggest circle be tangent to a side of the biggest triangle at say P where one of the endpoints of the side P is on is A. Then <OAP = 30 as it is equilateral, so AO/OP = 1/sin30 = 2. So AO = 2OP, but AO is the radius of the bigger circle, OP the radius of the smaller. So each circle has half the radius of the one before it. (this can also be proven by invoking Euler's formula for triangles:
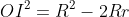
where O,I,R,r are the circumcentre, incentre, circumradius, inradius respectively.
We now find the ratio of the red area to the green area in just one annulus. So say take the biggest circle and triangle, and cut a hole where the next circle is. Say the radius of the big circle is one. Then the area of the triangle including the hole is 3*1/2*1*1*sin120 = (3root3)/4. Then, the red area is R = pi - (3root3)/4 and the green area is G = (3root3)/4 - pi/4.
We now find the final answer. All the red and green areas form a geometric series with ratio 1/4 since each circle is half the radius of the one before so areas are reduced to a quarter; so the total red area = R(1+1/4+1/16+...) = R/1-(1/4) = 4R/3. Similarly total green area = 4G/3. Then the final ratio is the same as R/G, i.e. it is
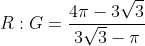
 >_>
>_>





