RealiseNothing
what is that?It is Cowpea
Last edited:
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
I will remove my post.Lets just give it away.
To me that final integral seems harder than the first...may be wrong though.

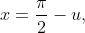

Can you give me a hint on how I can do that?

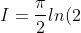)
That's usually how integrals are made up lols. But you should be careful because not all functions are integratable, but nearly all are differentiatable.A way to come up with really complicated integrals that can be done using elementary functions: make up a complicated function and differentiate it
For the cot one, is it a really obscure substitution of the difficulty of like x = (1-u)/(1+u)?To me that final integral seems harder than the first...may be wrong though.
Not the way I did it.For the cot one, is it a really obscure substitution of the difficulty of like x = (1-u)/(1+u)?
I am guessing I need to multiply 1 in a clever way, no?Not the way I did it.
Ok here is my attempt at proving the above equality.I am guessing I need to multiply 1 in a clever way, no?
I need to find a way to prove that:
I am considering some sort of periodicity argument but I don't think that might work.
Alright nice.Good solution Sy, pretty much the same speed as mine really:
Spiral's method was to letNow what's the elegant method!?
How does that lead to something faster than the previous solutions?Spiral's method was to let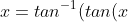))
idk I didn't actually try the method myself lol.How does that lead to something faster than the previous solutions?
Ah well, am interested to know.idk I didn't actually try the method myself lol.

