RealiseNothing
what is that?It is Cowpea
c) iii) This is just an integration by parts, I won't go through most of the working out as it is just straight forward IBP. However:
x}{2})}{\sin(\frac{x}{2})} dx)
Let}})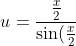
and thus )
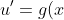(given)
Letx}{2}))
and thus x}{2})}{\frac{(4n-1)}{2}})
Put these into the IBP formula and evaluate the
, then factor out })
to obtain the result of:
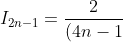}[1+ \lim_{a \to 0} \int_{a}^{\pi} g(x) \cos(\frac{(4n-1)x}{2}) dx])
c)iv) Now we know that \leq 1)
, hence we can deduce that:
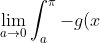 dx \leq \lim_{a \to 0} \int_{a}^{\pi} g(x) \cos(\frac{(4n-1)x}{2}) dx \leq \lim_{a \to 0} \int_{a}^{\pi} -g(x) dx)
Evaluating the upper and lower bounds gives:
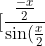}] \leq \lim_{a \to 0} \int_{a}^{\pi} g(x) \cos(\frac{(4n-1)x}{2}) dx \leq [\frac{\frac{x}{2}}{\sin(\frac{x}{2})}])
Now we know that} = 1)
so we evaluate using the limits and we get the required result:
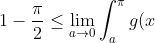 \cos(\frac{(4n-1)x}{2}) dx \leq \frac{\pi}{2} - 1)
c)v) As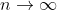
we get 
.
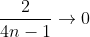Now as we established above, \cos(\frac{(4n-1)x}{2} dx )
is a finite as it is bounded between two finite values.
Thus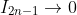
c)vi) We know now that as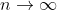 we get 
and so from part c)ii) we get:
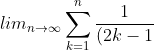^2} = \frac{\pi^2}{8})
Also we have:
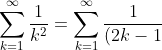^2}} + \sum_{k=1}^{\infty} \frac{1}{(2k)^2})
Substituting in our known value for the sum of the reciprocal odd squares, and factorising out a quarter from the last summation gives:
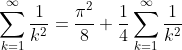
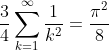
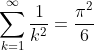
Let
Let
Put these into the IBP formula and evaluate the
c)iv) Now we know that
Evaluating the upper and lower bounds gives:
Now we know that
c)v) As
Now as we established above,
Thus
c)vi) We know now that as
Also we have:
Substituting in our known value for the sum of the reciprocal odd squares, and factorising out a quarter from the last summation gives:
Last edited:
