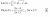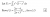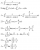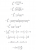-
Coming soon...BoS Trial exams Watch this space!
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012-14 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter bleakarcher
- Start date
- Status
- Not open for further replies.
Re: MX2 Integration Marathon

Ofcourse you did.Let's generalize that just a little bit
(its doable I tried it)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
Yep something like thatchucking a carrot I see
I got I(n)={[k(n-m+1)]/[m+k(n+1)]}I(n-m)
integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 776
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
Hey guys in dat UNSW ASOC integration bee, there was this weird question (carrot would approve)

Hey guys in dat UNSW ASOC integration bee, there was this weird question (carrot would approve)
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
The actual integration is very straightforward, it's just finding the closed form that not too many people are familiar with.
I thought it was a rather different one though lol.Hey guys in dat UNSW ASOC integration bee, there was this weird question (carrot would approve)

The actual integration is very straightforward, it's just finding the closed form that not too many people are familiar with.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
Hint: Let u = (that expression)Hey guys in dat UNSW ASOC integration bee, there was this weird question (carrot would approve)

Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon

nice workchange into half angles -> int{[x+2sin(x/2)cos(x/2)]/2cos^2(x/2) dx}
=int{1/2 [xsec^2(x/2)]+tan(x/2) dx}
=[xtan(x/2)] between x=0 and x=pi/4 by reverse product rule
=pi/4tan(pi/8)
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Last edited:
- Status
- Not open for further replies.