HSC 2015 MX2 Marathon (archive) (3 Viewers)

Ekman · Mar 13, 2015

Re: HSC 2015 4U Marathon

Is it ok to prove it like this?

$\frac{z+w}{z-w} \times \frac{\bar{z} - \bar{w}}{\bar{z} - \bar{w}}$

$= \frac{\bar{z}w - \bar{w}z}{2|z|^2 - (w\bar{z} + z\bar{w})}$

$\bar{z}w - \bar{w}z $ is purely imaginary$$

$\therefore \frac{z+w}{z-w} $ is purely imaginary$$

VBN2470 · Mar 13, 2015

Re: HSC 2015 4U Marathon

Yes, that should be fine too, as long as you can prove those other expressions are imaginary, the proof is valid.

FrankXie · Mar 14, 2015

Re: HSC 2015 4U Marathon

Chlee1998 said:
View attachment 31910

In the diagram, there are 3 circles which are all externally tangent to each other and a semi circle. The shaded area is equal to 120. find the unshaded area of the semi circle

$$ let the bigger circle have radius $ x $ and the smaller circle have radius $ y. $ so the semicircle has radius $ 2x.$
$$ Now we can establish the equation by Pythagoras $ (x+y)^2-(x-y)^2=(2x-y)^2-y^2.$
by finding the relationship between x and y, and using the given condition, the unshaded area is 40.

FrankXie · Mar 14, 2015

Re: HSC 2015 4U Marathon

Chlee1998 said:
the line from the center of the semi circle to the point where one of the small circles are tangent to the cyrved bit of the semi circle also goes rhrough the center of the small circle?

yes of course, because the semicircle and the smaller circle are also tangent(internally), the centres and the point of contact are colinear. isn't this a theorem in circle geometry?

Ekman · Mar 16, 2015

Re: HSC 2015 4U Marathon

Simple question:

$$What is the eccentricity of: $ \frac{y^2}{225} - \frac{x^2}{64}=1$

PhysicsMaths · Mar 16, 2015

Re: HSC 2015 4U Marathon

Ekman said:
Simple question:

$$What is the eccentricity of: $ \frac{y^2}{225} - \frac{x^2}{64}=1$

b^2 = a^2 (e^2-1),

e^2 = a^2+b^2/a^2
e = 17/15

Drsoccerball · Mar 16, 2015

Re: HSC 2015 4U Marathon

PhysicsMaths said:
b^2 = a^2 (e^2-1),

e^2 = a^2+b^2/a^2
e = 17/15

LOL. I lose a mark

Sy123 · Mar 16, 2015

Re: HSC 2015 4U Marathon

$\\ $Show that$ \ \log_{10}8 \ $is irrational$$

InteGrand · Mar 16, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $Show that$ \ \log_{10}8 \ $is irrational$$

Suppose $\log _{10}8=\frac{a}{b}$ , where a and b are coprime positive integers.

Then $10^{\frac{a}{b}}=8\Rightarrow 10^a=8^b$ .

This is a contradiction because the LHS ends in 0 in base 10, whereas the RHS cannot end in 0 (the last digits of powers of 8 go in the repeating cycle 8,4,2,6,8,4,2,6,8,....).

braintic · Mar 16, 2015

Re: HSC 2015 4U Marathon

InteGrand said:
Suppose $\log _{10}8=\frac{a}{b}$ , where a and b are coprime positive integers.

Then $10^{\frac{a}{b}}=8\Rightarrow 10^a=8^b$ .

This is a contradiction because the LHS ends in 0 in base 10, whereas the RHS cannot end in 0 (the last digits of powers of 8 go in the repeating cycle 8,4,2,6,8,4,2,6,8,....).

Why did you need the 'coprime' ?

PhysicsMaths · Mar 16, 2015

Re: HSC 2015 4U Marathon

Drsoccerball said:
LOL. I lose a mark

bl. I'm assuming you used a^2-b^2/a^2 ? (for ellipse)

InteGrand · Mar 16, 2015

Re: HSC 2015 4U Marathon

braintic said:
Why did you need the 'coprime' ?

I didn't for this proof, but I'm used to writing a rational number as a fraction in its lowest terms, so I wrote coprime without thinking too much about it.

Sy123 · Mar 17, 2015

Re: HSC 2015 4U Marathon

$\\ $Solve the following system of equations$ \\ \\ 2x_1 + x_2+x_3 + x_4 + x_5 = 6 \\ x_1 + 2x_2 + x_3+x_4+x_5 = 12 \\ x_1+x_2+2x_3+x_4+x_5 =24 \\ x_1+x_2+x_3+2x_4+x_5 = 48 \\ x_1+x_2+x_3+x_4+2x_5=96$

Fizzy_Cyst · Mar 17, 2015

Re: HSC 2015 4U Marathon

That was fun

I get:

x1 = -25
x2 = -19
x3 = -7
x4 = 17
x5 = 65

Fizzy_Cyst · Mar 17, 2015

Re: HSC 2015 4U Marathon

A car takes a banked curve of a racing track at p m/s, the lateral gradient angle $\phi$ being designed to reduce the tendency to side-slip to zero for a lower speed q.

Show that the coefficient of friction necessary to prevent side-slip for the greater speed p must be at least:

$\frac{(p^2-q^2) sin \phi cos \phi}{p^2sin^2\phi+q^2cos^2\phi}$

FrankXie · Mar 17, 2015

Re: HSC 2015 4U Marathon

Sy123 said:
$\\ $Solve the following system of equations$ \\ \\ 2x_1 + x_2+x_3 + x_4 + x_5 = 6 \\ x_1 + 2x_2 + x_3+x_4+x_5 = 12 \\ x_1+x_2+2x_3+x_4+x_5 =24 \\ x_1+x_2+x_3+2x_4+x_5 = 48 \\ x_1+x_2+x_3+x_4+2x_5=96$

adding up all five equations we obtain $6(x_1+x_2+x_3+x_4+x_5)=6(1+2+4+8+16)$ or $x_1+x_2+x_3+x_4+x_5=31$ then subtracting this equation from each of the original equations respectively

FrankXie · Mar 17, 2015

Re: HSC 2015 4U Marathon

Fizzy_Cyst said:
A car takes a banked curve of a racing track at p m/s, the lateral gradient angle $\phi$ being designed to reduce the tendency to side-slip to zero for a lower speed q.

Show that the coefficient of friction necessary to prevent side-slip for the greater speed p must be at least:

$\frac{(p^2-q^2) sin \phi cos \phi}{p^2sin^2\phi+q^2cos^2\phi}$

when the speed is q, no side force, we have $N_q\cos\phi=mg, N_q\sin\phi=mq^2/r$ which yields $gr=\frac{q^2}{\tan\phi}$ ....(1)

when the speed is p>q, the side force F is downwards, we have $N_p\cos\phi-F\sin\phi=mg, N_p\sin\phi+F\cos\phi=mp^2/r$ which (by dividing them) result in $\frac{p^2}{gr}=\frac{N_p\sin\phi+F\cos\phi}{N_p\cos\phi-F\sin\phi}=\frac{\tan\phi+F/N_p}{1-F/N_p\tan\phi}$ sub in the equation (1) for gr, and let $\mu=F/N_p$ which is the coefficient of friction, it follows $\frac{p^2\tan\phi}{q^2}=\frac{\tan\phi+\mu}{1-\mu\tan\phi}$ finally solving the last equation for 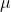$\mu$ completes the proof

FrankXie · Mar 17, 2015

Re: HSC 2015 4U Marathon

next question

$$ The hyperbola $ xy=c^2 $ meets the ellipse $ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ at $ P\left(ct_1,\frac{c}{t_1}\right) $ and $ Q\left(ct_2,\frac{c}{t_2}\right) $ where $ t_1>t_2>0. $ Tangents to the hyperbola at $ P $ and $ Q $ meet in $ T, $ while tangents to the ellipse at $ P $ and $ Q $ meet in $ V. $ (i) Show that the line $ TV $ passes through the origin. (ii) Show that if $ V $ lies at a focus of the hyperbola, then the ellipse is in fact a circle and find the radius of this circle in terms of $ c.$

Ekman · Mar 19, 2015

Re: HSC 2015 4U Marathon

FrankXie said:
next question

$$ The hyperbola $ xy=c^2 $ meets the ellipse $ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ at $ P\left(ct_1,\frac{c}{t_1}\right) $ and $ Q\left(ct_2,\frac{c}{t_2}\right) $ where $ t_1>t_2>0. $ Tangents to the hyperbola at $ P $ and $ Q $ meet in $ T, $ while tangents to the ellipse at $ P $ and $ Q $ meet in $ V. $ (i) Show that the line $ TV $ passes through the origin. (ii) Show that if $ V $ lies at a focus of the hyperbola, then the ellipse is in fact a circle and find the radius of this circle in terms of $ c.$

Loved it!

$(I)$ \frac{xct_1}{a^2} + \frac{yc}{b^2t_1} = 1 $ and $ \frac{xct_2}{a^2} + \frac{yc}{b^2t_2} = 1 $ are the two tangents of the ellipse$

$\therefore x(t_1 - t_2) + \frac{ya^2}{b^2}\times(\frac{1}{t_1} - \frac{1}{t_2}) = 0 $ is the locus of point T, and it passes through the origin as well.$$

$x\frac{c}{t_1} + yct_1 = 2c^2 $ and $ x\frac{c}{t_2} + yct_2 = 2c^2 $ are the two tangents of the hyperbola $$

$\therefore x(\frac{1}{t_1} - \frac{1}{t_2}) + y(t_1-t_2) = 0 $ is the locus of point V, and it passes through the origin as well. $$

$$ Gradient of the locus of T: $ t_1t_2\frac{b^2}{a^2} $ and the gradient of the locus of V: $ \frac{1}{t_1t_2}$

$\frac{(t_1)^2 - (t_2)^2}{a^2} + \frac{\frac{1}{(t_1)^2} - \frac{1}{(t_2)^2}}{b^2} = 0 $ Sub in points P and V into the ellipse and minus the two equations in order to achieve a relationship between a,b and $ t_1,t_2$

$\therefore \frac{b^2}{a^2} = \frac{1}{(t_1t_2)^2} \Rightarrow \frac{a}{b} = t_1t_2$

$\therefore $ Through simple substitution the gradients of point T and V are equal, thus O, T and V are collinear points and line VT passes through the origin$$

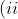$(ii)$ y=\frac{2c}{t_1+t_2} $ and $ x=\frac{2ct_1t_2}{t_1+t_2} $ are co-ordinates of point V$

$\therefore $ Since the foci of an hyperbola are: $ (\sqrt{2}c , \sqrt{2}c) $ and $ \frac{y}{x} = \frac{1}{t_1t_2} $ where y and x are the co-ordinates of V$$

$\frac{\sqrt{2}c}{\sqrt{2}c} = 1 = \frac{1}{t_1t_2}$

$Since $ t_1t_2 = \frac{a}{b} \therefore a=b $ through simple substitution$

$\therefore $ as $ a=b $ the ellipse becomes a circle$$

However, every time I try finding the radius of x^2 + y^2 = a^2 in terms of c, I keep on getting the same result of c being equal to 1...

Drsoccerball · Mar 21, 2015

Re: HSC 2015 4U Marathon

Can someone try this?:
$$ Find the locus of $ arg(z-2)+arg(z+2)=\pi$

HSC 2015 MX2 Marathon (archive) (3 Viewers)

Well-Known Member

Well-Known Member

Active Member

Active Member

Well-Known Member

Active Member

Well-Known Member

This too shall pass

Well-Known Member

Well-Known Member

Active Member

Well-Known Member

This too shall pass

Well-Known Member

Well-Known Member

Active Member

Active Member

Active Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 3)