Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,612
- Gender
- Male
- HSC
- 2015
Re: MX2 2015 Integration Marathon
 Rationalized the denominator.
Rationalized the denominator.

 (Through x=u^2 substitution)
(Through x=u^2 substitution)
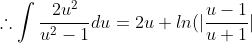 = 2\sqrt{x} + ln(|\frac{\sqrt{x}-1}{\sqrt{x}+1}|) )
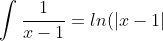 )
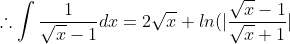 + ln(|x-1|) +c )
Edit: I just realized now:
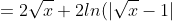 + c )
Edit: I just realized now:
Last edited:
