KingOfActing
lukewarm mess
Re: MX2 2016 Integration Marathon


After heaps of integration by parts our integral becomes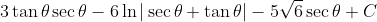
Then back substitution using and lots of simplification, our integral can be written as
and lots of simplification, our integral can be written as 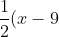\sqrt{x^2+2x+7} - 6\ln{|x+1 +\sqrt{x^2+2x+7}|} + C)
I just tried it but I think I made a mistake somewhereGet over it Paradox. When it comes to maths you're at latest a 15'er
-------------
Not sure if KingOfActing will go for it
After heaps of integration by parts our integral becomes
Then back substitution using




