Paradoxica
-insert title here-
Rules are as per the other marathons. Difficulty should be reasonable, and hints should be provided as deemed necessary. Use any "elementary" techniques, provided you state them, and if it's fairly advanced, outline a proof.
I'll start off simple.
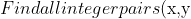$ that satisfy $x^2 + 6xy + 8y^2 +3x +6y = 2)
Other things:
For the purposes of this thread, the set of all natural numbers excludes zero.
Vectors and elementary functions of any kind are allowed, but little to no calculus. (this one due to leehuan)
Define terms that the average person following this thread probably wouldn't know.
State any theorems/techniques that may help in solving the problem.
I'll start off simple.
Other things:
For the purposes of this thread, the set of all natural numbers excludes zero.
Vectors and elementary functions of any kind are allowed, but little to no calculus. (this one due to leehuan)
Define terms that the average person following this thread probably wouldn't know.
State any theorems/techniques that may help in solving the problem.
Last edited:
