davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
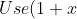^n= (1+x)(1+x)^{n-1} $ to prove that $ \dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1} )
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
The integral symbolically reduces to evaluatingHave you tried this one of Paradoxica's evil integrals: \sqrt { { x }^{ 4 }+2{ x }^{ 3 }+4{ x }^{ 2 }+2x+1 } }{ { x }^{ 2 }\left( x+1 \right) } dx } )
Do not consider the substitution right away. Split the integral apart by rationalising the denominator before attempting anything else, as you will obtain two fairly simple rational terms. Then proceed with the substitution.Trigonometric substitutions were already split off from simplistic substitutions in 4U/3U for the difficulty of having to sub back in. So I'm just going to spoil some of the answer.
And at this point I'm still not sure how this is done using only 3U methods
For some reason when I processed the rationalising method in my head it didn't yield something that was more simplified than the above result. May have to give it an actual attempt later.Do not consider the substitution right away. Split the integral apart by rationalising the denominator before attempting anything else, as you will obtain two fairly simple rational terms. Then proceed with the substitution.
can someone post a hard integration by substitution question, please
I don't think any of those exist.
I don't think any of those exist.
(x-2)^2}\,dx)
Well from what KoA has told me, the way he expects an X1 student to do it is through advanced algebraic manipulation.That csc^2(theta)sec(theta) was the most problematic one I observed for MX1. That's why I didn't seek to continue
I'm at school right now so I can't type it up, but the way to solve it is to NOT split the integral at all.
Keep it as is, until you end up with (sinθ +1)cosθ/((1-sinθ)sin^3(θ))
Now let u = sinθ
Next is adding and subtracting u or 2u for "partial fraction"ish part
BY ONLY SUBSTITUTION:I don't think any of those exist.
(x-2)^2}\,dx)
I'm sorry, but this just looked like gibberish.BY ONLY SUBSTITUTION:
(1/2)lnsecarctan(sqrt(x-2)/2)+lnsinarctan(sqrt(x-2)/2)-1/4csc^2arctan(sqrt(x-2)/2)-(1/2)lnsinarctan(sqrt(x-2)/2)+ln(secarctan(sqrt(x-2)/2)+tanarctan(sqrt(x-2)/2))+1/2lntanarctan(sqrt(x-2)/2)-cscarctan(sqrt(x-2)/2)
I think you might want to simplify a term or two...
By inspection....Does anyone know how to graph Rational Functions without drawing a table of values, and just by analysing the equation?
Well I know all the kinds up to the power of 3.By inspection....
Most exponential graphs don't require that many values...Well I know all the kinds up to the power of 3.
I mean up to infinity
I think you might want to simplify a term or two...
or all of them...

