HSC 2016 MX1 Marathon (archive) (4 Viewers)

davidgoes4wce · Mar 14, 2016

Re: HSC 2016 3U Marathon

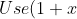$Use (1+x)^n= (1+x)(1+x)^{n-1} $ to prove that $ \dbinom{n}{k}=\dbinom{n-1}{k}+\dbinom{n-1}{k-1}$

$Answer: \dbinom{n-1}{k}+\dbinom{n-1}{k-1}$

Paradoxica · Mar 14, 2016

Re: HSC 2016 3U Marathon

leehuan said:
Have you tried this one of Paradoxica's evil integrals: $\int { \frac { \left( x-1 \right) \sqrt { { x }^{ 4 }+2{ x }^{ 3 }+4{ x }^{ 2 }+2x+1 } }{ { x }^{ 2 }\left( x+1 \right) } dx }$

The integral symbolically reduces to evaluating

$\int \frac{\sqrt{x^2+1}}{x+1}$d$x$

Paradoxica · Mar 14, 2016

Re: HSC 2016 3U Marathon

leehuan said:
Trigonometric substitutions were already split off from simplistic substitutions in 4U/3U for the difficulty of having to sub back in. So I'm just going to spoil some of the answer.

$\\ x-2=4\tan ^{ 2 }{ \theta } \Rightarrow dx=8\tan { \theta } \sec ^{ 2 }{ \theta }\, d\theta \\ \int { \frac { \sqrt { x+2 } +\sqrt { x-2 } }{ \left( \sqrt { x+2 } -\sqrt { x-2 } \right) { \left( x-2 \right) }^{ 2 } } dx } \\ =\int { \frac { \sqrt { 4+4\tan ^{ 2 }{ \theta } } +\sqrt { 4\tan ^{ 2 }{ \theta } } }{ \left( \sqrt { 4+4\tan ^{ 2 }{ \theta } } -\sqrt { 4\tan ^{ 2 }{ \theta } } \right) { \left( 4\tan ^{ 2 }{ \theta } \right) }^{ 2 } } \cdot 8\tan { \theta } \sec ^{ 2 }{ \theta } d\theta }$
$\\ =\int { \frac { \left( 2\sec { \theta } +2\tan { \theta } \right) }{ \left( 2\sec { \theta } -2\tan { \theta } \right) \left( 16\tan ^{ 4 }{ \theta } \right) } \cdot 8\tan { \theta } \sec ^{ 2 }{ \theta } d\theta } \\ =\frac { 1 }{ 2 } \int { \frac { \sec ^{ 2 }{ \theta } +2\sec { \theta } \tan { \theta } +\tan ^{ 2 }{ \theta } }{ \left( \sec ^{ 2 }{ \theta } -\tan ^{ 2 }{ \theta } \right) \left( \tan ^{ 3 }{ \theta } \right) } \sec ^{ 2 }{ \theta } d\theta } \\ =\frac { 1 }{ 2 } \int { \frac { 1+2\sin { \theta } +\sin ^{ 2 }{ \theta } }{ \sin ^{ 3 }{ \theta } \cos { \theta } } d\theta }$

And at this point I'm still not sure how this is done using only 3U methods

Do not consider the substitution right away. Split the integral apart by rationalising the denominator before attempting anything else, as you will obtain two fairly simple rational terms. Then proceed with the substitution.

leehuan · Mar 14, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
Do not consider the substitution right away. Split the integral apart by rationalising the denominator before attempting anything else, as you will obtain two fairly simple rational terms. Then proceed with the substitution.

For some reason when I processed the rationalising method in my head it didn't yield something that was more simplified than the above result. May have to give it an actual attempt later.

Carrotsticks · Mar 14, 2016

Re: HSC 2016 3U Marathon

KINGOM 885 said:
can someone post a hard integration by substitution question, please

KingOfActing said:
I don't think any of those exist.

$\\ $By using the substitution $ u=x $, find *difficult integral*.$$

Paradoxica · Mar 14, 2016

Re: HSC 2016 3U Marathon

$\int $d$x$

Paradoxica · Mar 14, 2016

Re: HSC 2016 3U Marathon

KingOfActing said:
I don't think any of those exist.

$$By considering the substitution $ x = 2 + 4\tan^2{\theta} $ or otherwise, find $ \int \frac{\sqrt{x+2}+\sqrt{x-2}}{(\sqrt{x+2}-\sqrt{x-2})(x-2)^2}\,dx$

$\frac{\log{(x-2)}}{2}-\frac{1}{x-2}+\int \frac{2\text{d}x}{\sin^2{\theta}\cos{\theta}}$

I'm not sure there is an obvious way to proceed for an X1 student.

leehuan · Mar 14, 2016

Re: HSC 2016 3U Marathon

That csc^2(theta)sec(theta) was the most problematic one I observed for MX1. That's why I didn't seek to continue

Paradoxica · Mar 14, 2016

Re: HSC 2016 3U Marathon

leehuan said:
That csc^2(theta)sec(theta) was the most problematic one I observed for MX1. That's why I didn't seek to continue

Well from what KoA has told me, the way he expects an X1 student to do it is through advanced algebraic manipulation.

Basically partial fractions by inspection.

KingOfActing · Mar 14, 2016

Re: HSC 2016 3U Marathon

I'm at school right now so I can't type it up, but the way to solve it is to NOT split the integral at all.

Keep it as is, until you end up with (sinθ +1)cosθ/((1-sinθ)sin^3(θ))

Now let u = sinθ

Next is adding and subtracting u or 2u for "partial fraction"ish part

leehuan · Mar 14, 2016

Re: HSC 2016 3U Marathon

KingOfActing said:
I'm at school right now so I can't type it up, but the way to solve it is to NOT split the integral at all.

Keep it as is, until you end up with (sinθ +1)cosθ/((1-sinθ)sin^3(θ))

Now let u = sinθ

Next is adding and subtracting u or 2u for "partial fraction"ish part

This is 3U. You have to give ALL the substitutions.

But yep I didn't think far enough to consider all the algebraic manipulations

Blitz_N7 · Mar 15, 2016

Re: HSC 2016 3U Marathon

KingOfActing said:
I don't think any of those exist.

$$By considering the substitution $ x = 2 + 4\tan^2{\theta} $ or otherwise, find $ \int \frac{\sqrt{x+2}+\sqrt{x-2}}{(\sqrt{x+2}-\sqrt{x-2})(x-2)^2}\,dx$

BY ONLY SUBSTITUTION:
(1/2)lnsecarctan(sqrt(x-2)/2)+lnsinarctan(sqrt(x-2)/2)-1/4csc^2arctan(sqrt(x-2)/2)-(1/2)lnsinarctan(sqrt(x-2)/2)+ln(secarctan(sqrt(x-2)/2)+tanarctan(sqrt(x-2)/2))+1/2lntanarctan(sqrt(x-2)/2)-cscarctan(sqrt(x-2)/2)

leehuan · Mar 15, 2016

Re: HSC 2016 3U Marathon

Blitz_N7 said:
BY ONLY SUBSTITUTION:
(1/2)lnsecarctan(sqrt(x-2)/2)+lnsinarctan(sqrt(x-2)/2)-1/4csc^2arctan(sqrt(x-2)/2)-(1/2)lnsinarctan(sqrt(x-2)/2)+ln(secarctan(sqrt(x-2)/2)+tanarctan(sqrt(x-2)/2))+1/2lntanarctan(sqrt(x-2)/2)-cscarctan(sqrt(x-2)/2)

I'm sorry, but this just looked like gibberish.

Paradoxica · Mar 15, 2016

Re: HSC 2016 3U Marathon

Blitz_N7 said:
$$\noindent$\frac{1}{2}\log{\left(\sec{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2}\right)}\right)}\right)}+$ $\log{\left(\sin{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2}\right)}\right)}\right)}-$ $\frac{1}{4}\csc^2{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2}\right)}\right)}-$ $\frac{1}{2}\log{\left(\sin{\left(\tan^{-1}{\frac{\sqrt{x-2}}{2}}\right)}\right)}+$ $\log{\left(\sec{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2} \right )} \right )} \right )}+$ $\tan{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2}\right)} \right )}+$ $\frac{1}{2}\log{\left(\tan{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2} \right)} \right )} \right )}-$ $\csc{\left(\tan^{-1}{\left(\frac{\sqrt{x-2}}{2} \right )} \right )}$

I think you might want to simplify a term or two...

or all of them...

si2136 · Mar 15, 2016

Re: HSC 2016 3U Marathon

Does anyone know how to graph Rational Functions without drawing a table of values, and just by analysing the equation?

Paradoxica · Mar 15, 2016

Re: HSC 2016 3U Marathon

si2136 said:
Does anyone know how to graph Rational Functions without drawing a table of values, and just by analysing the equation?

By inspection....

si2136 · Mar 15, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
By inspection....

Well I know all the kinds up to the power of 3.

I mean up to infinity

Paradoxica · Mar 15, 2016

Re: HSC 2016 3U Marathon

si2136 said:
Well I know all the kinds up to the power of 3.

I mean up to infinity

Most exponential graphs don't require that many values...

Blitz_N7 · Mar 15, 2016

Re: HSC 2016 3U Marathon

Paradoxica said:
I think you might want to simplify a term or two...

or all of them...

$\ln\left(\sqrt{x+2}+\sqrt{x-2}\right)-\sqrt{\dfrac{x+2}{x-2}}+\dfrac{x+2}{8-4x}+\dfrac{\ln\left(x-2\right)}{2}$

leehuan · Mar 18, 2016

Re: HSC 2016 3U Marathon

$$Use the inverse function theorem to find $\frac{d}{dx}\sec^{-1}{x} \\ $Verify your answer by redefining $y=\sec^{-1}{x}$

HSC 2016 MX1 Marathon (archive) (4 Viewers)

Well-Known Member

-insert title here-

-insert title here-

Well-Known Member

Retired

-insert title here-

-insert title here-

Well-Known Member

-insert title here-

lukewarm mess

Well-Known Member

Member

Well-Known Member

-insert title here-

Well-Known Member

-insert title here-

Well-Known Member

-insert title here-

Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 4)