leehuan's All-Levels-Of-Maths SOS thread (3 Viewers)

seanieg89 · Mar 28, 2016

Drsoccerball said:
$What I would do (which is probably wrong) :$

$$ Consider cases if $ f(x) \rightarrow 0 $ as $ x \rightarrow a $ and $ f(x) \rightarrow \infty $ as $ x \rightarrow b$

$$ Then there is a minimum value between $ (0,\infty ) $ since $ f(x) >0 $ there is such a y value $ c $ which $ f(x) \geq c \ \in c (b,a)$

$$ Similarly for if $ a \rightarrow b \ , b \rightarrow a$

This post makes no sense. How can f(x) tend to infinity at b? By continuity it has to tend to f(b) there.

And how have you deduced that a minimum exists? That is almost precisely what you need to prove.

Also b and a are the endpoints of a fixed interval, why are you talking about b -> a ?

leehuan · Mar 28, 2016

seanieg89 said:
Call it the extreme value theorem, the term "max-min" and "min-max" occur a ton in other contexts.

How you should prove it will depend on exactly what you have learned, typically you assume this theorem without proof in most first year courses. (For good reason, discussion of things like compactness distract a bit from learning calculus which is the main point of first year calculus course).

Have you heard of any of the following?

-Compactness
-Bolzano-Weierstrass theorem
-Heine Borel theorem

Only heard of, never taught. Very well, will assume

seanieg89 · Mar 28, 2016

leehuan said:
Only heard of, never taught. Very well, will assume

Yes, best to do this for now.

A sketch of a possible proof though (about the lowest-tech one I can think of off the top of my head, although also the least general):

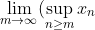Given a sequence of real numbers, we define the limit superior of the sequence as $\lim_{m\rightarrow\infty}(\sup_{n\geq m} x_n)$ . (You definitely will need to know what the supremum "sup" of a set of real numbers is, the existence of supremums for bounded sets is pretty much the defining property of the reals.)

You can prove the limit superior of any bounded sequence of reals exists by the monotone convergence theorem.

A corollary of this is that any bounded sequence of reals has a convergent subsequence.

Now suppose the c in your question did not exist. Then you could find a sequence x_n with f(x_n)->0.

Pass to a convergent subsequence y_n, and we must still have f(y_n)->0.

If y is the limit of y_n, then f(y)=0 by continuity. This contradicts the positivity of f and completes the proof.

leehuan · Mar 29, 2016

InteGrand · Mar 29, 2016

leehuan said:
$$Suppose that $f$ is continuous on the closed interval $\left[0,1\right]$ and that $0\le f\left(x\right) \le 1$ for every $x \in \left[0,1\right]$. Show that there exists a real number $c \in \left[0,1\right]$ such that $f\left(c\right)=c$

$The question said: Otherwise, use the intermediate value theorem to $g(x)=f(x)-x\\$This method is straightforward, but what would be another method. They said: \\ Hint: If $f(0)=0$ or $f(1)=1$ we are done.$

If f(0) = 0 or f(1) = 1, we are done (taking c = 0 or c = 1 respectively does the job).

Otherwise, apply the intermediate value theorem to g (which is continuous as it is the difference of two continuous functions), noting that g(0) and g(1) are of opposite signs, because g(0) = f(0) and g(1) = f(1) – 1 (recall the range of f). So there is a c in (0, 1) such that g(c) = 0, i.e. f(c) = c.

leehuan · Mar 29, 2016

Oh my bad. Misread the question, didn't realise the "otherwise" bit belonged to the ENTIRE hint.

leehuan · Mar 30, 2016

InteGrand · Mar 30, 2016

leehuan said:
$\\$Suppose $f$ is a continuous function on the interval $\left[0,1\right]$ and that $f\left(0\right)=f\left(1\right)\\$Let $n\in \mathbb {Z}^{+},n\neq 1$. Show that \\ $\exists \, a\in\left[0,1\right]\Rightarrow f\left(a\right)=f\left(a+\frac{1}{n}\right)$

$\noindent This question was answered here $\Big{(}$With $a$ needing to be in $\left[0,1-\frac{1}{n}\right]$$\Big{)}$:$

http://community.boredofstudies.org...1437/intermediate-value-theorem-question.html.

leehuan · Mar 30, 2016

Somehow I typoed the question. Yes a was meant to be between 0 and 1-1/n

I got some algebra homework to do though, so if anyone has the time after LaTeX stops messing up on this website can someone please do me a huge favour fix Sy's invalid equation for the alternate method please?

leehuan · Mar 30, 2016

Paradoxica · Mar 30, 2016

Impossible. sinh(3x) can be written strictly in terms of sinh(x)

sin^3(x) cannot possibly be written as a polynomial in terms of coshx, let alone sinh(x)

leehuan · Mar 30, 2016

That's what I thought. Which makes me want to crunch this past paper up because they dared to put in a dud question.

leehuan · Mar 30, 2016

The boring method is just to sub all components in and prove the equality, or convert the corresponding matrix into it's R-E form.

Is there a way to attempt the following question with some properties of matrices.

E.g. If v and w are solutions of Ax=b, then v-w is a solution of Ax=0

Question:
$\\ $Show that $\bf{x}=\left(\begin{matrix}7\\2 \\ 0 \end{matrix} \right)+\lambda\left(\begin{matrix}-2\\0\\1\end{matrix}\right),\lambda \in \mathbb R$ are the solutions of$$
$\begin{align*}{x}_{1}-2{x}_{2}+2{x}_{3}&=3\\2{x}_{1}-6{x}_{2}+4{x}_{3}&=2\\-2{x}_{1}+4{x}_{2}-4{x}_{3}&=-6\end{align*}$

$\\$and that $\bf{x}=\lambda\left(\begin{matrix}-2\\0\\1\end{matrix}\right),\lambda \in \mathbb R$ are the solutions of the corresponding homogeneous system$ \\ \begin{align*}{x}_{1}-2{x}_{2}+2{x}_{3}&=0\\2{x}_{1}-6{x}_{2}+4{x}_{3}&=0\\-2{x}_{1}+4{x}_{2}-4{x}_{3}&=0\end{align*}$

Drsoccerball · Mar 30, 2016

leehuan said:
$\\ $Show that $\bf{x}=\left(\begin{matrix}7\\2 \\ 0 \end{matrix} \right)+\lambda\left(\begin{matrix}-2\\0\\1\end{matrix}\right),\lambda \in \mathbb R$ are the solutions of$$
$\begin{align*}{x}_{1}-2{x}_{2}+2{x}_{3}&=3 \rightarrow (1)\\ 2{x}_{1}-6{x}_{2}+4{x}_{3}&=2 \rightarrow (2) \\-2{x}_{1}+4{x}_{2}-4{x}_{3}&=-6 \rightarrow (3) \end{align*}$

$Take note that $ (1) $ and $ (3) $ are equal.$

$Sub in point $\left(\begin{matrix}7\\2 \\ 0 \end{matrix} \right) $ into (1) and (2) and notice the equations hold.$

$$ Now notice that the vector equation is in the form $ \overrightarrow{x}= \overrightarrow{A} +\lambda_1 \overrightarrow{AB} \ $ or $ \overrightarrow{x}= \overrightarrow{A} +\lambda_1 \overrightarrow{BA}$

$Now sub in the value for B into both the equations (1) and (2) and notice the equations hold.$

$\therefore $ the vector equation is the solution of (1),(2),(3).$

$Q.E.D$

EDIT: Woops didn't see your comment.

InteGrand · Mar 30, 2016

leehuan said:
The boring method is just to sub all components in and prove the equality, or convert the corresponding matrix into it's R-E form.

Is there a way to attempt the following question with some properties of matrices.

E.g. If v and w are solutions of Ax=b, then v-w is a solution of Ax=0

Question:
$\\ $Show that $\bf{x}=\left(\begin{matrix}7\\2 \\ 0 \end{matrix} \right)+\lambda\left(\begin{matrix}-2\\0\\1\end{matrix}\right),\lambda \in \mathbb R$ are the solutions of$$
$\begin{align*}{x}_{1}-2{x}_{2}+2{x}_{3}&=3\\2{x}_{1}-6{x}_{2}+4{x}_{3}&=2\\-2{x}_{1}+4{x}_{2}-4{x}_{3}&=-6\end{align*}$

$\\$and that $\bf{x}=\lambda\left(\begin{matrix}-2\\0\\1\end{matrix}\right),\lambda \in \mathbb R$ are the solutions of the corresponding homogeneous system$ \\ \begin{align*}{x}_{1}-2{x}_{2}+2{x}_{3}&=0\\2{x}_{1}-6{x}_{2}+4{x}_{3}&=0\\-2{x}_{1}+4{x}_{2}-4{x}_{3}&=0\end{align*}$

Convert the linear system into an augmented matrix, then get this to row echelon form using Gaussian Elimination. You can then check whether solutions exist by observing the right-hand column. If solutions exist, you can proceed to find them in parametric form by setting any non-leading column variables equal to a free parameter and solving for the other variables from the rows of the row-echelon matrix. This is the standard procedure for solving linear systems using matrices.

Drongoski · Mar 30, 2016

Another way:

Generate a second point from the vector equation of the line: say take lambda = 2 ==> point is B(3,2,2)

Therefore we have 2 points on the line, viz: A(7, 2, 0) and B(3,2,2)

By showing these 2 points satisfy these 2 equation we show they lie on the 2 planes (1) and (2). Since these 2 planes are not identical, the only way this can happen is that points A and B lie on the given line must also lie on the line of intersection of the 2 planes; i.e. this given line is the intersection of (1) and (2) and of course (3).

Of course the usual way would be to perform the Gaussian elimination as described by InteGrand above.

leehuan · Mar 30, 2016

Well yeah, but when I said convert R-E form I was actually implying Gaussian Elimination. I only called it boring because whilst it's rote, it's something I've done one too many times.

Possibly Drongoski's solution was what I wanted.

But to clarify further, the question was slotted under an exercise that taught me some elementary properties of matrices like the one above. Will post these said properties later if I remember to.
I was just wondering if manipulation of those properties would've been beneficial.

This is because, the first matrix is in the form [A|b] but the second matrix is in the form [A|0] where A = A. So I wasn't sure if the solutions related somehow in a convenient manner.

InteGrand · Mar 30, 2016

leehuan said:
Well yeah, but when I said convert R-E form I was actually implying Gaussian Elimination. I only called it boring because whilst it's rote, it's something I've done one too many times.

Possibly Drongoski's solution was what I wanted.

But to clarify further, the question was slotted under an exercise that taught me some elementary properties of matrices like the one above. Will post these said properties later if I remember to.
I was just wondering if manipulation of those properties would've been beneficial.

This is because, the first matrix is in the form [A|b] but the second matrix is in the form [A|0] where A = A. So I wasn't sure if the solutions related somehow in a convenient manner.

They are related; the part containing the lambda in the non-homogeneous case is precisely the solution to the homogeneous case (not by coincidence).

In general, if we have a consistent (i.e. solvable) non-homogeneous system Ax = b, the solution will be the form x = x_p + x_h, where x_p is any particular solution to the system, and x_h is the general solution to the homogeneous case (and yes, this can be proved using properties of matrices; you may wish to try to do so as an exercise). So in your particular problem's case, the part containing the lambda is the solution of the homogeneous case.

Drongoski · Mar 31, 2016

A more direct alternative to my post above: (call the 3 variables x, y and z and let w represent lambda):

The given vector equation implies: x = 7 - 2w; y = 2; z = w

You find the 3 equations all satisfied (of course plane 3 is just plane 1):

For (1): LHS = (7-2w) - 2 x 2 + 2w = 7 - 2w - 4 + 2w = 3

For (2): LHS = 2 x (7-2w) - 6 x 2 + 4w = 14 - 4w - 12 + 4w = 2

So the given vector eqn of the line satisfies the 3 linear eqns for any lambda.

leehuan · Mar 31, 2016

leehuan's All-Levels-Of-Maths SOS thread (3 Viewers)

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

-insert title here-

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 3)