Pretty sure this is an old Tournament of Towns problem but wasn't too difficult (maybe IMOSL G1?)... It is a bit of a pain to convert to directed angles so left as an exercise to the reader.
We construct midpoints
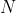
,
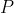
,
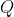
of
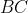
,
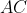
,
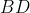
respectively. Also, let
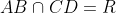
,
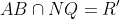
and
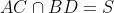
. By Midpoint Theorem, we have
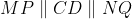
and
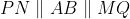
so
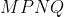
is a parallelogram with
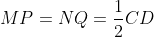
and
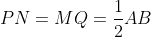
. Since
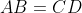
, we have
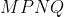
is a rhombus.
Furthermore, since
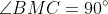
,
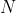
is the centre of the circle passing through
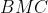
by semicircle theorem. Thus,
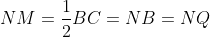
as
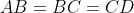
. Therefore,
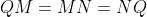
and
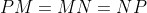
so
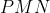
and
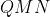
are equilateral triangles. In particular,
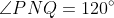
.
As a result of these parallel lines, we have
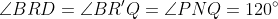
, so
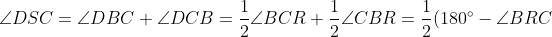 = 30^{\circ})
.
Thus, the angle between the diagonals is
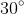
, so the area of
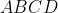
is
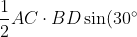 = \frac{1}{4} AC \cdot BD)
.
