-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Pls help (1 Viewer)
- Thread starter =)(=
- Start date
ExtremelyBoredUser
Bored Uni Student
Could you give the whole question? This seems like it requires prior context to do since in theory a regular parabola within a certain domain for k would suffice?
The only way for a parabola to touch but not cross a circle is if the two have common tangents at each of the points of intersection, and thus a double root where the curves meet. So, the question is asking for  such that
such that ^2 = 1) , a quartic, has two double roots.
, a quartic, has two double roots.
First we have to solve the two equations simultaneously so that the zeros of that equation are the points of intersection.

Sub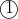 into
into 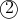
^2=1\\x^2+x^4-2x^2k+k^2=1\\x^4+(1-2k)x^2+(k^2-1)=0)
Since the two graphs touch each other at two points, there will be two double roots which we'll label as
Sum of roots:

Sum of product of pairs:

Product of roots:

From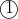 we get
we get  , sub that into
, sub that into 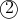

Sub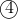 and
and  into
into 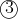
^2=\left (\frac{2\alpha^2+1}{2} \right )^2-1\\\\\alpha^4=\left (\frac{4\alpha^4+4\alpha^2+1}{4} \right)-1\\\\\alpha^4=\alpha^4+\alpha^2+\frac{1}{4}-1\\\\\alpha^2-\frac{3}{4}=0)
}}{2}\text{Using quadratic formula})

To find the value of k we can just sub alpha and beta into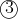
^2+4\left(\frac{\sqrt{3}}{2}\right)\left(-\frac{\sqrt{3}}{2}\right)+\left(-\frac{\sqrt{3}}{2}\right)^2=1-2k\\\\\frac{3}{4}-3+\frac{3}{4}=1-2k\\\\k=\frac{-\frac{3}{2}-1}{-2}\\\\k=\frac{5}{4})
Now to find the points at which the graph touch each other we just sub the values of alpha and beta into the original equation.
^2-\frac{5}{4}\\\\y=-\frac{1}{2})
^2-\frac{5}{4}\\\\y=-\frac{1}{2})
Therefore points of contact are\ \text{and}\ \left(\frac{\sqrt{3}}{2},\ -\frac{1}{2}\right)) and
and 
Sub
Since the two graphs touch each other at two points, there will be two double roots which we'll label as
Sum of roots:
Sum of product of pairs:
Product of roots:
From
Sub
To find the value of k we can just sub alpha and beta into
Now to find the points at which the graph touch each other we just sub the values of alpha and beta into the original equation.
Therefore points of contact are
An identical question (with a couple of different values) was previously asked. It was as follows:
Two roots of
The working out for this question is included below:


You should use this as guidance to solve your question (i.e. using the appropriate values from your own question).
Important edit:
As @CM_Tutor kindly pointed out, the working out attached should actually say to look at the roots of 14, which are
I hope this helps!
Last edited:
I suspect it is more efficient to recognise this as a quadratic inFirst we have to solve the two equations simultaneously so that the zeros of that equation are the points of intersection.
Subinto
^2=1\\x^2+x^4-2x^2k+k^2=1\\x^4+(1-2k)x^2+(k^2-1)=0)
Now, if there is a solution to this equation with
Perhaps more elegantly, examining
The attachment should actually say to look at the roots of 14, which are
Thank you for pointing this out! I have adjusted my post to reflect thisThe attachment should actually say to look at the roots of 14, which are, and not the roots of 34. Further, the roots of 34 are incorrectly stated, as they should be
. Likely a couple of typos here.




