-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
2022 CSSA MATH EXT 2 Thoughts (1 Viewer)
- Thread starter Flise
- Start date
16 b: ProveCouldn't solve 16aii) and Q16b)
Q16a)
Q16b) Consider the concavity of y=(x)^1/3
Prove (a-b)^1/3 + (a+b)^1/3 < 2(a)^1/3
Any ideas?
Looking at the graph
for all x in the positive reals, meaning it is concave down always for
Using a concave down function and letting
Also, 16a is basically identical to one of the questions in my tutorial sheet for uni and is categorized as a hard one as well. CSSA did the same thing last year with polynomials and proving factor theorem.
Last edited:
Flise
Member
- Joined
- Jan 22, 2022
- Messages
- 59
- Gender
- Male
- HSC
- 2022
16ci) There was a part one which was to find v in terms of t given resistance is kv^2, mass of skydiver is 'm', and take up as positive (weirdly)
Basically integrating a = 1/m (kv^2 - mg), note: assume at rest when t=0
They give you the required result:
)
Part two gives you values and wants you to find the time when the skydiver is 1500m from the ground
Dropped from an altitude of 5000m, mass = 100kg, k=0.25, g=10
I integrated the equation to get x in terms of t but was stuck thereafter.
Basically integrating a = 1/m (kv^2 - mg), note: assume at rest when t=0
They give you the required result:
Part two gives you values and wants you to find the time when the skydiver is 1500m from the ground
Dropped from an altitude of 5000m, mass = 100kg, k=0.25, g=10
I integrated the equation to get x in terms of t but was stuck thereafter.
Last edited:
Couldn't get out 16 a) and b); besides that everything was fine...
That's okay I guess. 16 c) for my school was replaced since we haven't finished mechanics.
Definitely was way harder than last years - last year's question 16 was an absolute snore.
That's okay I guess. 16 c) for my school was replaced since we haven't finished mechanics.
Definitely was way harder than last years - last year's question 16 was an absolute snore.
Flise
Member
- Joined
- Jan 22, 2022
- Messages
- 59
- Gender
- Male
- HSC
- 2022
Also what did yall get for the distance travelled for Q15b) the fricken vector-helix question combined with mechanics. My unwise brain saw it was 1 mark and I just did the velocity (4m/s) times 10 (since they wanted after 10s)! Surely it wasn't that simple...
I too got that. It was just length; not distance; and it was also a 1 marker, so yeah, it was that simple. Was probably trying to catch out some people trying to over-complicate it. That question was fun.Also what did yall get for the distance travelled for Q15b) the fricken vector-helix question combined with mechanics. My unwise brain saw it was 1 mark and I just did the velocity (4m/s) times 10 (since they wanted after 10s)! Surely it wasn't that simple...
I really enjoyed the Question 14; reduction formulae question. Was a satisfying result.
How were you supposed to do the first Complex Numbers question of Question 15? I don't know if I did it right.
subbing in the given values you get16ci) There was a part one which was to find v in terms of t given resistance is kv^2, mass of skydiver is 'm', and take up as positive (weirdly)
Basically integrating a = 1/m (kv^2 - mg), note: assume at rest when t=0
They give you the required result:
Part two gives you values and wants you to find the time when the skydiver is 1500m from the ground
Dropped from an altitude of 5000m, mass = 10kg, k=0.25, g=10
I integrated the equation to get x in terms of t but was stuck thereafter.
Integrating from t=0 ->T
I feel like somethings wrong
It was a relationship between the roots ofI too got that. It was just length; not distance; and it was also a 1 marker, so yeah, it was that simple. Was probably trying to catch out some people trying to over-complicate it. That question was fun.
I really enjoyed the Question 14; reduction formulae question. Was a satisfying result.
How were you supposed to do the first Complex Numbers question of Question 15? I don't know if I did it right.
Last edited:
Flise
Member
- Joined
- Jan 22, 2022
- Messages
- 59
- Gender
- Male
- HSC
- 2022
I'm so pissed I screwed up my conversion of -1 into exponential form.I too got that. It was just length; not distance; and it was also a 1 marker, so yeah, it was that simple. Was probably trying to catch out some people trying to over-complicate it. That question was fun.
I really enjoyed the Question 14; reduction formulae question. Was a satisfying result.
How were you supposed to do the first Complex Numbers question of Question 15? I don't know if I did it right.
I wrote z^9 = cis(kpi) instead of z^9 = cis(pi + 2kpi) I'm so dumbbb. All you then do is sum of roots, one of the roots comes out as ±1/2 and just make note of -cos5pi/9 = cos4pi/9 and -cos7pi/9 = cos2pi
Flise
Member
- Joined
- Jan 22, 2022
- Messages
- 59
- Gender
- Male
- HSC
- 2022
Btw the question was z^9+1 = 0It was a relationship between the roots ofi.e you factorise it and get
and then you let them equal 0
and luckily each of the roots have corresponding conjugates and hence adding each of the roots the imaginary parts go away and you just get left with the
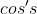
Flise
Member
- Joined
- Jan 22, 2022
- Messages
- 59
- Gender
- Male
- HSC
- 2022
My bad mass was 100kg ain't a baby skydivingsubbing in the given values you get
Integrating from t=0 ->T
I feel like somethings wrong
Flise
Member
- Joined
- Jan 22, 2022
- Messages
- 59
- Gender
- Male
- HSC
- 2022
I'm so pissed as well for this question I literally did a variation of it three nights ago sinx + sin2x + ... + sinnx but literally mindblanked for part ii)I too got that. It was just length; not distance; and it was also a 1 marker, so yeah, it was that simple. Was probably trying to catch out some people trying to over-complicate it. That question was fun.
I really enjoyed the Question 14; reduction formulae question. Was a satisfying result.
How were you supposed to do the first Complex Numbers question of Question 15? I don't know if I did it right.
I got part i) luckily it was just a geometric progression, but I couldn't simplify the result...
I divided each term by e^itheta/2 when I was suppose to do that only for the bottom, while the top required me factoring e^i(ntheta) which I couldn't see in the exam!!
Last edited:
