-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Question (1 Viewer)
- Thread starter ProGT408
- Start date
synthesisFR
afterhscivemostlybeentrollingdonttakeitsrsly
Cuz for Part a u do (z^2)^3 - 1 = 0a) fully factorise z^6-1=0 over the rational field
b) solve z^2+z^4+z^6 over the complex field
how do you use part a to do part b?
Then use the difference of two cubes formula thing ye
For part b factorise z^2 out to get 1 + z^2 + z^4 which is in the bracket of the part a one mad ting innit
Then use the solutions from a to get the ones in part two by doing normal roots of unit minus the solution z=1 cus that’s the other bracket cuh
Then u basically get the rest of the solutions fam
Free the mandem while your at it
liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,102
- Gender
- Female
- HSC
- 2023
for a) z^6-1 = 0 -> (z^3-1)(z^3+1)=0 -> (z-1)(z^2+z+1)(z+1)(z^2-z+1)=0 using difference of squares, now z^2+z+1 and z^2-z+1 have complex roots so we do not factorise any furthera) fully factorise z^6-1=0 over the rational field
b) solve z^2+z^4+z^6 over the complex field
how do you use part a to do part b?
then for b) using a) to expand some brackets: (z-1)(z+1)(z^4+z^2+1)=0
hence the solutions to z^4+z^2+1 = 0 are the complex 6ths roots of units, namely those with modulus 1 and argument pi/3, 2pi/3, -pi/3, and -2pi/3 (since z = -1, z = 1 are the solutions to z-1 = 0, z+1 = 0, meaning z^4+z^2+1 must have the other solutions to z^6 = 1)
now z^2+z^4+z^6 = z^2 (z^4 + z^2 +1) hence the solutions are z = 0 and the complex 6th roots of unity above
ivanradoszyce
Member
- Joined
- Oct 18, 2023
- Messages
- 61
- Gender
- Undisclosed
- HSC
- 2018
For part a), write
 as
as 
a difference of 2 cubes.
Recall that(a^2 + ab + b^2)) , therefore
, therefore (z^4 + z^2 + 1) )
The roots where are
are  .
.
b) Consider
 as
as 
In this case we need to find the 6th roots of unity. So let , there for
, there for  .
.

Therefore

For the Principle Argument of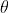


Therefore , which means
, which means 
The values of and
and 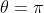 , represent the values of
, represent the values of 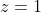 and
and 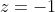
The values of are the solutions to
are the solutions to
Let's now consider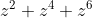
 &=0 \\
z^2(x^4 + z^2 + 1) &=0 \\
\end{align*}
)
Using the results from part (a)
, z = cis \; \left(-\frac{\pi}{3} \right) , z = cis \; \left(-\frac{\pi}{3} \right), z = cis \; \left(-\frac{2\pi}{3} \right)$}
\end{align*}
)
a difference of 2 cubes.
Recall that
The roots where
b) Consider
In this case we need to find the 6th roots of unity. So let
Therefore
For the Principle Argument of
Therefore
The values of
The values of
Let's now consider
Using the results from part (a)
Recognising the GP in the second polynomial allows the link between the two parts to be seen more easily:
^3 - 1\right]}{z^2 - 1} &= 0 \qquad \text{on summing the GP with $a = z^2$, $r = z^2$, and $n = 3$} \\ \frac{z^2\left(z^6 - 1\right)}{z^2 - 1} &= 0 \\ z^2\left(z^6 - 1\right) &= 0 \qquad \text{provided $z^2 - 1 \neq 0$} \end{align*})
Henxe, the roots of are the six roots of
are the six roots of  , with the two roots of
, with the two roots of  , that is, at
, that is, at  , removed, and a double root at
, removed, and a double root at 
Henxe, the roots of

