Question (1 Viewer)
- Thread starter ProGT408
- Start date
synthesisFR
afterhscivemostlybeentrollingdonttakeitsrsly
Cuz for Part a u do (z^2)^3 - 1 = 0
Then use the difference of two cubes formula thing ye
For part b factorise z^2 out to get 1 + z^2 + z^4 which is in the bracket of the part a one mad ting innit
Then use the solutions from a to get the ones in part two by doing normal roots of unit minus the solution z=1 cus that’s the other bracket cuh
Then u basically get the rest of the solutions fam
Free the mandem while your at it
liamkk112
Well-Known Member
- Joined
- Mar 26, 2022
- Messages
- 1,061
- Gender
- Female
- HSC
- 2023
for a) z^6-1 = 0 -> (z^3-1)(z^3+1)=0 -> (z-1)(z^2+z+1)(z+1)(z^2-z+1)=0 using difference of squares, now z^2+z+1 and z^2-z+1 have complex roots so we do not factorise any further
then for b) using a) to expand some brackets: (z-1)(z+1)(z^4+z^2+1)=0
hence the solutions to z^4+z^2+1 = 0 are the complex 6ths roots of units, namely those with modulus 1 and argument pi/3, 2pi/3, -pi/3, and -2pi/3 (since z = -1, z = 1 are the solutions to z-1 = 0, z+1 = 0, meaning z^4+z^2+1 must have the other solutions to z^6 = 1)
now z^2+z^4+z^6 = z^2 (z^4 + z^2 +1) hence the solutions are z = 0 and the complex 6th roots of unity above
ivanradoszyce
Member
- Joined
- Oct 18, 2023
- Messages
- 43
- Gender
- Undisclosed
- HSC
- 2018
For part a), write
as 
a difference of 2 cubes.
Recall that(a^2 + ab + b^2))
, therefore (z^4 + z^2 + 1) )
The roots where
are 
.
b) Consider
as 
In this case we need to find the 6th roots of unity. So let
, there for 
.
Therefore
For the Principle Argument of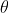
Therefore
, which means 
The values of
and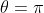 
, represent the values of 
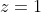and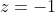 
The values of
are the solutions to
Let's now consider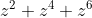
 &=0 \\
z^2(x^4 + z^2 + 1) &=0 \\
\end{align*}
)
Using the results from part (a)
, z = cis \; \left(-\frac{\pi}{3} \right) , z = cis \; \left(-\frac{\pi}{3} \right), z = cis \; \left(-\frac{2\pi}{3} \right)$}
\end{align*}
)
a difference of 2 cubes.
Recall that
The roots where
b) Consider
In this case we need to find the 6th roots of unity. So let
Therefore
For the Principle Argument of
Therefore
The values of
The values of
Let's now consider
Using the results from part (a)
Recognising the GP in the second polynomial allows the link between the two parts to be seen more easily:
^3 - 1\right]}{z^2 - 1} &= 0 \qquad \text{on summing the GP with $a = z^2$, $r = z^2$, and $n = 3$} \\ \frac{z^2\left(z^6 - 1\right)}{z^2 - 1} &= 0 \\ z^2\left(z^6 - 1\right) &= 0 \qquad \text{provided $z^2 - 1 \neq 0$} \end{align*})
Henxe, the roots of
are the six roots of 
, with the two roots of 
, that is, at 
, removed, and a double root at 
Henxe, the roots of