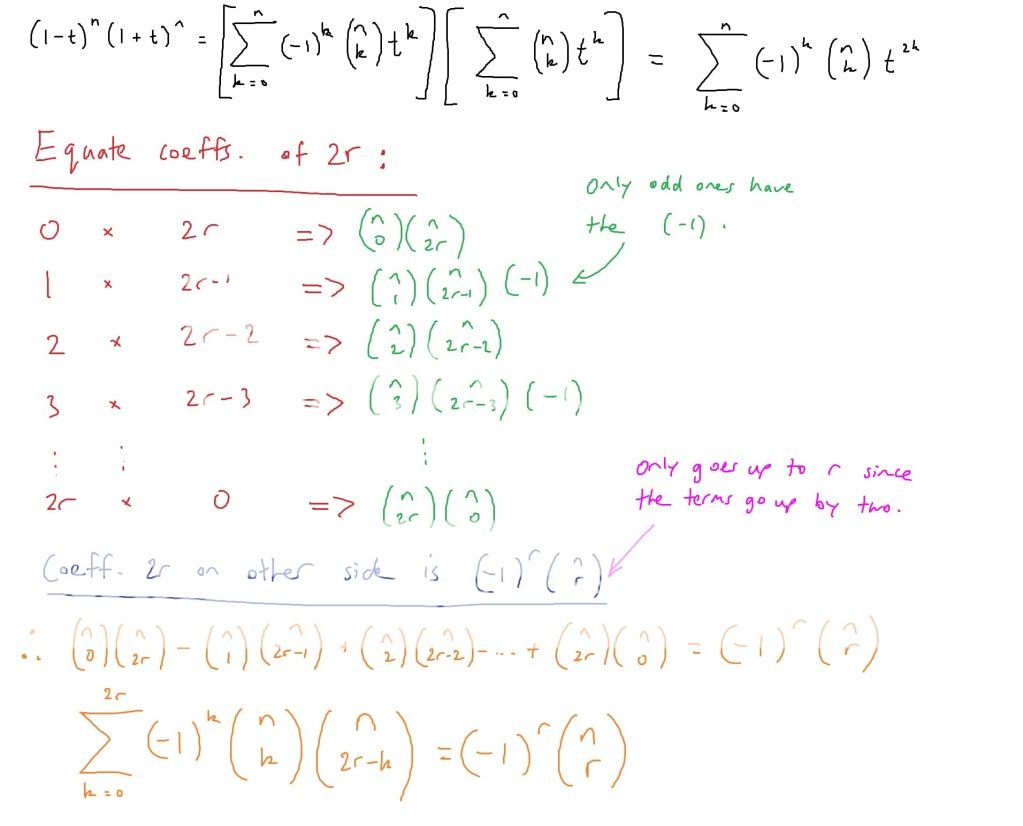-
Looking for HSC notes and resources? Check out our Notes & Resources page 
Binomial Theorem (1 Viewer)
- Thread starter goobi
- Start date
fortune_cookie
Banned
- Joined
- May 18, 2012
- Messages
- 193
- Gender
- Undisclosed
- HSC
- N/A
EDIT: you compare coeffiecents of t^(2r). Can't be bothered, it's midnight.
Also, this is from the 2007 Catholic Trial HSC. If you have this question , you would already have the solution.
Also, this is from the 2007 Catholic Trial HSC. If you have this question , you would already have the solution.
Last edited:
fortune_cookie
Banned
- Joined
- May 18, 2012
- Messages
- 193
- Gender
- Undisclosed
- HSC
- N/A
LHS = (nC0-nC1 t + nC2 t^2 -nC3 t^3 +nC4 t^4 - ...... +nCn (-t)^n) (nC0+nC1 t +nC2 t^2 + ....+ nCn t^n)
Coefficent of t^2 = nC0 nCn -nC1 nCn-1 +nC2 nCn-2 - .....
Coefficent of t^2 = nC0 nCn -nC1 nCn-1 +nC2 nCn-2 - .....
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
Thanks Carrotsticks
This probably sounds very stupid but I wonder how you multiply the two summations in the first line (as I haven't learnt it yet). Shouldn't the term
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
That does not sound stupid at all.Thanks Carrotsticks
This probably sounds very stupid but I wonder how you multiply the two summations in the first line (as I haven't learnt it yet). Shouldn't the termbe squared also?
I didn't actually multiply the two summations explicitly, that would have been FAR too tedious and long. Which C(n,k) did you think should be squared? I ask this because I have a couple up there. Were you referring to the C(n,k) from the expansion of (1-t^2)^n?
All I did in the first line was write both of the series out in Sigma notation because I personally prefer Sigma notation over expanded notation (although occasionally expanded form has its advantages) and I wanted to express both series in a more 'compact' form (not to be confused with 'closed form').
All I did was pick out the necessary terms that yield t^2r.
ie: t^0 x t^2r = t^2r etc
And by doing so, we of course multiply the coefficients, which is exactly what I did after the ===> symbol.
goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
I was referring to the C(n,k) from the expansion of L.H.S.That does not sound stupid at all.
I didn't actually multiply the two summations explicitly, that would have been FAR too tedious and long. Which C(n,k) did you think should be squared? I ask this because I have a couple up there. Were you referring to the C(n,k) from the expansion of (1-t^2)^n?
All I did in the first line was write both of the series out in Sigma notation because I personally prefer Sigma notation over expanded notation (although occasionally expanded form has its advantages) and I wanted to express both series in a more 'compact' form (not to be confused with 'closed form').
All I did was pick out the necessary terms that yield t^2r.
ie: t^0 x t^2r = t^2r etc
And by doing so, we of course multiply the coefficients, which is exactly what I did after the ===> symbol.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
No, it should not be squared.
I didn't actually multiply the two terms, hence it is not squared.
Even if I did multiply the two terms, it would be incorrect to say [C(n,k)]^2 because k is the 'bound variable'.
That's like me saying:

Which is most certainly incorrect.
I didn't actually multiply the two terms, hence it is not squared.
Even if I did multiply the two terms, it would be incorrect to say [C(n,k)]^2 because k is the 'bound variable'.
That's like me saying:
Which is most certainly incorrect.
goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
So how did you get t^2k in the first line then if you "didn't actually multiply the two terms"? That's what confuses meNo, it should not be squared.
I didn't actually multiply the two terms, hence it is not squared.
Even if I did multiply the two terms, it would be incorrect to say [C(n,k)]^2 because k is the 'bound variable'.
That's like me saying:
Which is most certainly incorrect.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
I just used the definition of the Binomial Expansion.So how did you get t^2k in the first line then if you "didn't actually multiply the two terms"? That's what confuses me
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 248
- Gender
- Male
- HSC
- 2013
Not necessarily. What if OP was given the question from his/her teacher in a revision booklet or something as such?EDIT: you compare coeffiecents of t^(2r). Can't be bothered, it's midnight.
Also, this is from the 2007 Catholic Trial HSC. If you have this question , you would already have the solution.
Bored_of_HSC
Active Member
- Joined
- Jul 9, 2011
- Messages
- 1,498
- Gender
- Female
- HSC
- 2012
Goobi plsThanks Carrotsticks
This probably sounds very stupid but I wonder how you multiply the two summations in the first line (as I haven't learnt it yet). Shouldn't the termbe squared also?
- Joined
- Feb 16, 2005
- Messages
- 8,405
- Gender
- Male
- HSC
- 2006
Um...looking at the first line of Carrotstick's solutions, the expansion should look like this:
^n(1+t)^n = \left(\displaystyle\sum_{i=0}^n \binom{n}{i}(-1)^i t^i \right)\left(\displaystyle\sum_{j=0}^n \binom{n}{j}t^j \right) = \displaystyle\sum_{i=0}^n \displaystyle\sum_{j=0}^n \binom{n}{i}\binom{n}{j}(-1)^i t^{i+j})
then you examine every combination of i + j = 2r...
The reason for that you can multiply the terms together is because you are effectively multiplying two general terms together when you expand the thing manually and finding every variation of i + j where i = {0, 1, .... , n} and j = {0, 1, .... , n}. Another way to see this is to note that in general, the double sigma means that
)
Note that the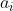 term in the brackets do not vary with each j so it can be factored out of the sum so we get
term in the brackets do not vary with each j so it can be factored out of the sum so we get
)
Now we can look at the sum outside as we vary i. Notice that the other summation term with j's in the square brackets does not change as we vary i, so we can factorise it outside the sum.
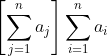
Now it should be clear that this leads to
 \left(\displaystyle\sum_{j=1}^n a_j\right))
then you examine every combination of i + j = 2r...
The reason for that you can multiply the terms together is because you are effectively multiplying two general terms together when you expand the thing manually and finding every variation of i + j where i = {0, 1, .... , n} and j = {0, 1, .... , n}. Another way to see this is to note that in general, the double sigma means that
Note that the
Now we can look at the sum outside as we vary i. Notice that the other summation term with j's in the square brackets does not change as we vary i, so we can factorise it outside the sum.
Now it should be clear that this leads to
Last edited:
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 248
- Gender
- Male
- HSC
- 2013
I am confused Trebla. Is the above relevant to the question, or is it just to demonstrate to goobi what happens when you multiply two summations?
- Joined
- Feb 16, 2005
- Messages
- 8,405
- Gender
- Male
- HSC
- 2006
The latter...I am confused Trebla. Is the above relevant to the question, or is it just to demonstrate to goobi what happens when you multiply two summations?
iSplicer
Well-Known Member
goobi pls.
Any help would be appreciated
But yeah, nice work Carrotsticks =D