RealiseNothing
what is that?It is Cowpea
Was the sneakiest thing ever.
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Most of the "obvious" proofs would be invalid.How was it sneaky?
Yes.Are you talking about 13d) ?
Damn!!!!!!!!!!!!!!!!!!!! I did thatMost of the "obvious" proofs would be invalid.
A lot of people would have assumed it was a straight line and done alternate angles.
Most of the "obvious" proofs would be invalid.
A lot of people would have assumed it was a straight line and done alternate angles.
I did that whilst knowing it was wrong coz I had no other method of doing it lolMost of the "obvious" proofs would be invalid.
A lot of people would have assumed it was a straight line and done alternate angles.
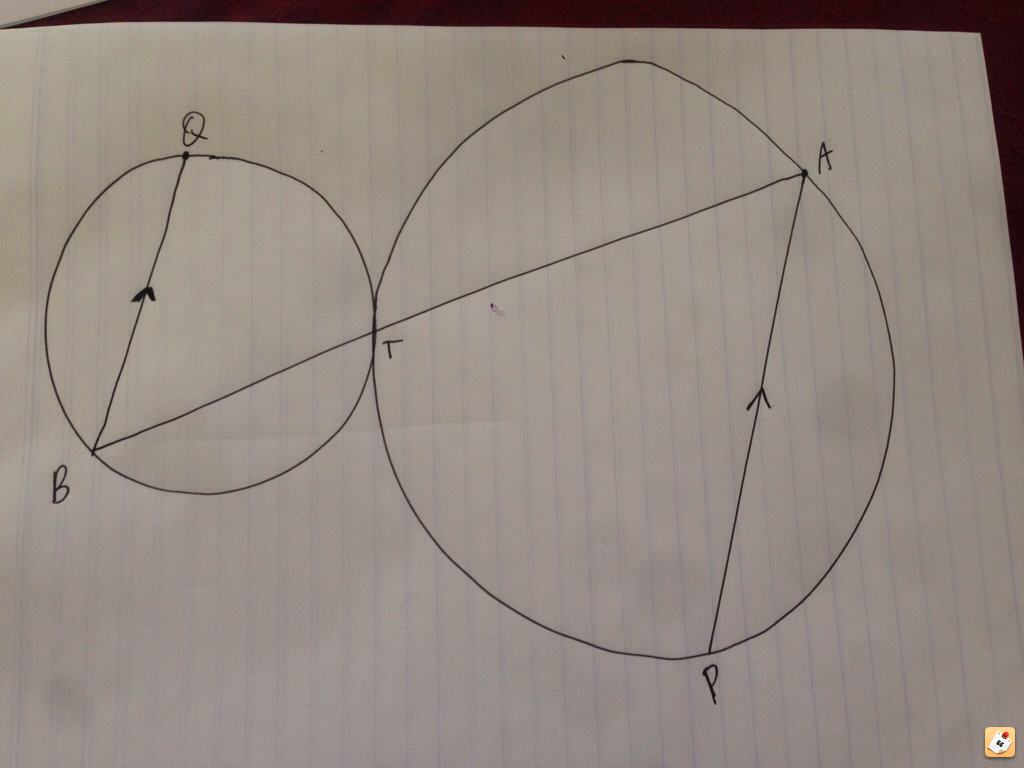
This is what I did.Draw a tangent through the point of intersection, then use angle in alternate segment theorem and vertically opposite angles (angles between the line you are given and your tangent) and prove the two alternate angles are equal therefore must be collinear
I'm always late to the party :'(Draw a tangent through the point of intersection, then use angle in alternate segment theorem and vertically opposite angles (angles between the line you are given and your tangent) and prove the two alternate angles are equal therefore must be collinear
I think that's fine.if you did alternate angles from the tangent drawn between the two circles, the proof would be valid right? you're proving that both angles produced from the tangent to their respective lines are equal -> therefore lies on the same line / co-linear.. I think..
I did this. Glad I'm not the only one.Draw a tangent through the point of intersection, then use angle in alternate segment theorem and vertically opposite angles (angles between the line you are given and your tangent) and prove the two alternate angles are equal therefore must be collinear
Is there a copy of the paper or question uploaded anywhere?Was the sneakiest thing ever.
Is there a copy of the paper or question uploaded anywhere?
Lol, that's why you should choose usydHey iBibah, doesn't it remind you of the UNSW seminar back in January.
Where like EVERYONE, including the 3rd year maths students, assumed it was a straight line.
de ja vu
