krypticlemonjuice
Member
- Joined
- Jun 24, 2023
- Messages
- 92
- Gender
- Male
- HSC
- 2023
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
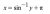
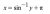 we are actually shifting it to the right by pi units because when we look at its inverse in the last line y = sin^-1(x-pi) which is a movement of pi units to the right. Thus we add pi to our extremities in the domain and the answer becomes: [pi/2,3pi/2].
we are actually shifting it to the right by pi units because when we look at its inverse in the last line y = sin^-1(x-pi) which is a movement of pi units to the right. Thus we add pi to our extremities in the domain and the answer becomes: [pi/2,3pi/2].Ahhh thanks so much that makes senseThis was from the Gosford Ext 1 paper that I was doing 2 days ago so I can definetly help you out with this one !!!
In my opinion the domain is incorrect. Actually if you rearrange to make x the subject in the last line you get:
View attachment 38964
consider y=sin^-1(x)
now inverse sin of y is the inverse function of:
y= sin^-1(x)
so it will aquire a range [-1,1] because we swap the domain and the range when finding an invere function.
So the domain of our function will be [-pi/2,pi/2] so when we consider View attachment 38964 we are actually shifting it to the right by pi units because when we look at its inverse in the last line y = sin^-1(x-pi) which is a movement of pi units to the right. Thus we add pi to our extremities in the domain and the answer becomes: [pi/2,3pi/2].
This is definetly a much better answer then mine cuz I went a bit too much into the detail lol. howcanibesmarter explains it in a nicer way... I would suggest you look at hers... its more conciseSo if you look at the original dy/dx = sqrt(1-y^2),
1-y^2 must be greater or equal to zero to be defined. Solving for y gives u the region of [-1,1]
Now plugging those values into the y=sin(x-pi) you get that domain for x, this matches SB257 answer
I hope that makes sense
