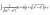Help me prove this standard form please (1 Viewer)

[WEMG]

I was doing a question in the Cambridge 4u textbook and came across a question which used the standard form below:



I have never came across this before and the textbook doesnt have the proof...
I was wondering if anyone could prove it for me.

Thanks!

 

[Aquawhite]

Are you only interested in how to do the proof, because it is given to you on the standard integrals sheet and hence won't have to know the proof or know the conversation by heart... just how to use it.

Sorry, I don't actually know the proof though.

 

[Drongoski]

I was doing a question in the Cambridge 4u textbook and came across a question which used the standard form below:



I have never came across this before and the textbook doesnt have the proof...

For integral to end up with that expression means if you differentiate w.r.t. x that expression you should get back the integrand: 1/sqrt(x^2 - a^2)
which you indeed will thus: d/dx[ln{x + sqrt(a^2-a^2)}] =

(1/x + sqrt(x^2 - a^2)) . [1 + 0.5(x^2 - a^2)^[-0.5] .2x] = the integrand

So this means, if you like, you can reverse this process to get the derivation for the integral formula.

That is - you have a proof.


EDIT: I've forgotten how to & I'm too dumb to figure out how/where I can access the LaTeX facility.
Can someone help out so I can post in LaTeX again. Or do I need to go back to using TeX

 

[Pwnage101]

1).Use the substituion x=a(sec(u))
2). To integrate sec(u) with respect to u note that d/du{sec(u)+tan(u)}=sec(u)[sec(u)+tan(u)], hence multiplying sec(u) by {sec(u)+tan(u)}/{sec(u)+tan(u)} will make things nice.
3). To transform the result from the variable u to x, draw up a right angled triangle
4). Use log-laws to reduce the expression so that all constants (i.e. terms that do not involve x) come under the constant of integration

Have a go. If you're still stuck, i'm sure many will help further.

 

[cutemouse]

It's easier if you use hyperbolic functions. But that's 1st year uni material.

 

[Trebla]

 

[jet]

It's easier if you use hyperbolic functions. But that's 1st year uni material.

Depends really. IMO they require about the same amount of work. Once you integrate you still need to convert from the inverse trig form to logarithmic form.