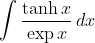-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Higher Level Integration Marathon & Questions (1 Viewer)
- Thread starter leehuan
- Start date
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
^ That was good practice!
I need to go out for dinner v soon, so will supply gory details later. In short, the answer can be expressed solely in terms of Apery's constant zeta(3).
1. IBP to essentially reduce the integral to log^2(1+x)/x. (The bulk of the difficulty of the originally posted integral lies in this integral as I see it.)
2. Expand this out to obtain an expression in terms of polylogs of order 2 and 3, but we basically only need to know the value of these polylogs at 1/2 and 1.
3. Special functions funtimes proving some reflection formulae etc to compute these guys.
I need to go out for dinner v soon, so will supply gory details later. In short, the answer can be expressed solely in terms of Apery's constant zeta(3).
1. IBP to essentially reduce the integral to log^2(1+x)/x. (The bulk of the difficulty of the originally posted integral lies in this integral as I see it.)
2. Expand this out to obtain an expression in terms of polylogs of order 2 and 3, but we basically only need to know the value of these polylogs at 1/2 and 1.
3. Special functions funtimes proving some reflection formulae etc to compute these guys.
Paradoxica
-insert title here-
I was looking for a polylog-free solution, but I guess this puts the nail on the coffin^ That was good practice!
I need to go out for dinner v soon, so will supply gory details later. In short, the answer can be expressed solely in terms of Apery's constant zeta(3).
1. IBP to essentially reduce the integral to log^2(1+x)/x. (The bulk of the difficulty of the originally posted integral lies in this integral as I see it.)
2. Expand this out to obtain an expression in terms of polylogs of order 2 and 3, but we basically only need to know the value of these polylogs at 1/2 and 1.
3. Special functions funtimes proving some reflection formulae etc to compute these guys.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Eh I wouldn't say that necessarily, I did the integral in a not particularly imaginative way...there could be a clever shortcut.I was looking for a polylog-free solution, but I guess this puts the nail on the coffin
To me it does seem like computing this integral is roughly the same mathematical "depth" as computing some particular values of the di/trilogarithm though.
Anyway, is there a reason why you were seeking to avoid them?
Paradoxica
-insert title here-
because I like a nice balance of low tech and efficient solutions to integralsEh I wouldn't say that necessarily, I did the integral in a not particularly imaginative way...there could be a clever shortcut.
To me it does seem like computing this integral is roughly the same mathematical "depth" as computing some particular values of the di/trilogarithm though.
Anyway, is there a reason why you were seeking to avoid them?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Fair enough, seems a rather subjective matter...to me polylog and polygamma manipulations are okay, but I also have no qualms about using contour integration etc.because I like a nice balance of low tech and efficient solutions to integrals
because I like a nice balance of low tech and efficient solutions to integrals
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
(Try ignoring the lengthy 4U way in this thread)
Last edited:
Paradoxica
-insert title here-
Prove the integral diverges if the argument of the exponential does not describe an ellipse.
Challenge: Formulate a generalisation to the above integral in higher dimensions. (Experience with Linear Algebra will be very handy)
Last edited:
Prove the integral diverges if the argument of the exponential does not describe an ellipse.
Challenge: Formulate a generalisation to the above integral in higher dimensions. (Experience with Linear Algebra will be very handy)
Paradoxica
-insert title here-
An answer that isn't an answer....
(As in you technically didn't do the computation, not that you're being cryptic)
Well I did say I was sketching a method (i.e. not giving the full answer).An answer that isn't an answer....
(As in you technically didn't do the computation, not that you're being cryptic)
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Oh didn't see you edited it, was the divergence thing always there and I just blind before?
In any case, we can still represent the quadratic form by a symmetric, hence diagonalisable matrix Q. If the quadratic form does not represent an ellipse, then at least one eigenvalue is non-positive, which implies that at least one of the integrals in the above product of single-variable integrals is infinite and we are done.
In any case, we can still represent the quadratic form by a symmetric, hence diagonalisable matrix Q. If the quadratic form does not represent an ellipse, then at least one eigenvalue is non-positive, which implies that at least one of the integrals in the above product of single-variable integrals is infinite and we are done.
I think it was there before. I remember answering it in my head but then forgetting to comment on it in my post. HahaOh didn't see you edited it, was the divergence thing always there and I just blind before?
In any case, we can still represent the quadratic form by a symmetric, hence diagonalisable matrix Q. If the quadratic form does not represent an ellipse, then at least one eigenvalue is non-positive, which implies that at least one of the integrals in the above product of single-variable integrals is infinite and we are done.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Easy difficulty