hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
That will probably not work, this is beyond HSC difficulty though (but within the scope of the syllabus)int(f(x))=int((f(a-x))?
Had a feeling there would be recursion, took me a while to find it:That will probably not work, this is beyond HSC difficulty though (but within the scope of the syllabus)
The answer is, it uses recursion in the solution, I can post my one on request
-----------------

Step back, davo's sol^n is like crazy. Sy did u have to mess around with identities as well or something else?That will probably not work, this is beyond HSC difficulty though (but within the scope of the syllabus)
The answer is, it uses recursion in the solution, I can post my one on request
-----------------

Yea his solution was pretty much exact same as mineStep back, davo's sol^n is like crazy. Sy did u have to mess around with identities as well or something else?
Alright, while i'm here...
Let t=tan(x/2)
Now casually using partial fractions...
At which point I basically ceebs typing the rest up, but should be integratable now easily.
.In this question we compute the Dirichlet integral using high school methods.
Note: n ranges over the non-negative integers.
Just a minor mistake... From your working:
Did not think of that, if you let u=arccot(3x^2) then you end up with a ln? Are both correct?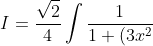^2} \cdot arccot(\3x^2) \cdot d(3x^2) )
Can someone pose a new question, on my behalf, please.
You are correct. There should be a negative. When I tentatively started doing it, I thought there ought to be a negative. I then flipped thru 2 text books for the derivative of arccot x - looking out for the '-' sign. Both times I did not see the '-'sign. After seeing your feedback, I rechecked both and there was the '-'sign. How I missed it both times yesterday baffles me. It must mean my glasses are not working as well as I thought.Also, in regards to the working, derivative of arccotx=negative * 1/1+x^2. So i believe there is a negative missing.
Where does this 'ln' come from ???Epic.
So, If i let u=arctan(3x^2) right, i get sqrt(2)/4 * ln(arctan(3x^2)) which if you derive also get a constant multiple of the integrand, so i assume both are correct.
Whoops I took cot inverse x= 1/tan inverse xWhere does this 'ln' come from ???
