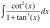integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 776
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
right......................

You can't use the limiting sum formula here since it diverges at x = pi/2 (or the indefinite integral which is tan x is undefined at pi/2)in your case, it'll be in terms of 'k' [i.e. (2k+1)/2^(2k+1)], since that's what you chose to represent as the index of summation