Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX1 Marathon #1 (archive) (1 Viewer)
- Thread starter nightweaver066
- Start date
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon

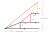
Given that tanx=3, where x is acute, find the values of
(i) Cosx
How do you start/ set out this question.

RivalryofTroll
Sleep Deprived Entity
- Joined
- Feb 10, 2011
- Messages
- 3,804
- Gender
- Male
- HSC
- 2013
- Uni Grad
- 2019
Re: 2012 HSC MX1 Marathon
sinx/cosx = 3
sin^2x/cos^2x = 9
1-cos^2x/cos^2x = 9
1-cos^2x = 9cos^2x
10cos^2x = 1
cos^2x = 1/10
cosx = Yeah!
I think this is right?
cosx = Square root (1/10)
tan x = 3Given that tanx=3, where x is acute, find the values of
(i) Cosx
How do you start/ set out this question.
sinx/cosx = 3
sin^2x/cos^2x = 9
1-cos^2x/cos^2x = 9
1-cos^2x = 9cos^2x
10cos^2x = 1
cos^2x = 1/10
cosx = Yeah!
I think this is right?
cosx = Square root (1/10)
RivalryofTroll
Sleep Deprived Entity
- Joined
- Feb 10, 2011
- Messages
- 3,804
- Gender
- Male
- HSC
- 2013
- Uni Grad
- 2019
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
If I had the money, I would personally buy everybody who posts in this thread a graphics tablet.
If I had the money, I would personally buy everybody who posts in this thread a graphics tablet.
Re: 2012 HSC MX1 Marathon
Haha would come in handy.If I had the money, I would personally buy everybody who posts in this thread a graphics tablet.
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Why not?If I survive maths extension 1 by the HSC I will thank you guys so much. Not even thinking about extension 2 anymore lol
Re: 2012 HSC MX1 Marathon
Doing 4U helps immensely with your 3U skills, plus it's a lot more fun. It's still early days, plenty of time to improve.
That is an extremely poor attitude to have and you won't succeed with it.If I survive maths extension 1 by the HSC I will thank you guys so much. Not even thinking about extension 2 anymore lol
Doing 4U helps immensely with your 3U skills, plus it's a lot more fun. It's still early days, plenty of time to improve.
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
Not to mention it means that 3U counts for 2 units.That is an extremely poor attitude to have and you won't succeed with it.
Doing 4U helps immensely with your 3U skills, plus it's a lot more fun. It's still early days, plenty of time to improve.
Compared to the people on this forum it might not be. Yet. The "maths people" here are pretty elite. You've got people in their first/second year of university maths, people who've competed in the international maths olympiad, Spiral and (iirc) someone that's about to start a Phd in maths in the US. They've had much, much more experience in maths than most people, so it's not really fair on you to compare yourself to them. I often feel intimdated by their far superior abilities, and I'm pretty sure lots of other people on this forum do as well.I've realised compared to everybody else my mathematics skill is nothing.
Last edited:
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
You should also realise that we're all in year 12 and there's the occasional university student posting in here.I've realised compared to everybody else my mathematics skill is nothing.
Re: 2012 HSC MX1 Marathon
Hmm I guess so, though with some questions I just look at them and think "WTF DOES THIS EVEN MEAN?"You should also realise that we're all in year 12 and there's the occasional university student posting in here.
Re: 2012 HSC MX1 Marathon
I was like that at the start of Year 11 when I was using the forums. Ohexploitable and hscishard, among others, knew a lot more maths than I did because they'd studied ahead and all that yet I'd only done what the class had done. It took a long time before I was finally able to understand all the questions that were asked - got to be patient.Hmm I guess so, though with some questions I just look at them and think "WTF DOES THIS EVEN MEAN?"
RivalryofTroll
Sleep Deprived Entity
- Joined
- Feb 10, 2011
- Messages
- 3,804
- Gender
- Male
- HSC
- 2013
- Uni Grad
- 2019
Re: 2012 HSC MX1 Marathon
Everything looks hard now but when you do it then yeah, everything becomes clear!
:/ Don't worry I feel the same too!Hmm I guess so, though with some questions I just look at them and think "WTF DOES THIS EVEN MEAN?"
Everything looks hard now but when you do it then yeah, everything becomes clear!
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
right.2Cos(360-48) = 2cos48 right/wrong?