-
Want to level up your HSC prep on those harder Maths questions? Register now for the BoS Trials (7th October)!
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX1 Marathon #1 (archive) (2 Viewers)
- Thread starter nightweaver066
- Start date
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
 ...) and then I'll have a go.
...) and then I'll have a go.
Don't worry Mr. Carrotsticks. I just have to finish my belonging essay (I knowlol nobody has yet tried my question ='(
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
I leave you with more things to ponder.

=\lim_{x \to a }g(x)=0, \pm \infty)
}{g'(x)} \ \textup{exists then})
}{g(x)}=\lim_{x \to a }\frac{f'(x)}{g'(x)}})

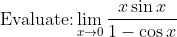
^\frac{1}{\ln x})
Have to dash and do some Physics, I will attempt the questions afterwards. (Be back at 9 PM) Keep them coming!
I leave you with more things to ponder.
Have to dash and do some Physics, I will attempt the questions afterwards. (Be back at 9 PM) Keep them coming!
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Here you go


Here you go


Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Wait a second... this looks like the Ruse Extension 2 2011 paper lol.Next question:

Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Thus A + B + C = arctan(0) = pi
I'm only saying this because my tablet just broke down lol.
Use the tan(A+B) thing where tanA=5 and tanB = 3, but twice. After some simplification, we have tan(A+B+C) = 0.Correct! But Ext. 1 students can do it.
Thus A + B + C = arctan(0) = pi
I'm only saying this because my tablet just broke down lol.
Re: 2012 HSC MX1 Marathon
I'd be very careful about tanning and then arc tanning it since you need to consider the restrictions between -pi/2 and pi/2. Probably should include an argument about it.
Just to clarify carrotsticks, is one of your steps:
arctan (-4/7) + arctan (4/7)?
I'd be very careful about tanning and then arc tanning it since you need to consider the restrictions between -pi/2 and pi/2. Probably should include an argument about it.
Just to clarify carrotsticks, is one of your steps:
arctan (-4/7) + arctan (4/7)?
RishBonjour
Well-Known Member
- Joined
- Aug 14, 2011
- Messages
- 1,261
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
Did you guys finish the whole course already? FUCK I'm SO BEHIND
ohh yeah, and lazy
Did you guys finish the whole course already? FUCK I'm SO BEHIND
ohh yeah, and lazy
zeebobDD
Member
- Joined
- Oct 23, 2011
- Messages
- 411
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX1 Marathon
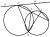
Last Q of one of our mx1 papers ;
Two circles intersect at A and B. P is a point on the first circle and Q is a point on the second circle such that PAQ is a straight line. C is a point on the second circle. The tangent to the first circle at P meets QC produced to R.
Prove that PBCR is a cyclic quadrilateral
Last Q of one of our mx1 papers ;
Two circles intersect at A and B. P is a point on the first circle and Q is a point on the second circle such that PAQ is a straight line. C is a point on the second circle. The tangent to the first circle at P meets QC produced to R.
Prove that PBCR is a cyclic quadrilateral
Sanical
SpiderAnderson
Re: 2012 HSC MX1 Marathon

Construct BA and point D (I forgot to write point Q which is produced from PA and lies on second circle)
let /_DPB = x
/_PAB = x (angle between tangent and chord equal to angle in alternate segment)
/_BAQ = 180 - x (adjacent supplementary angles)
/_BCQ = 180 - x (angles equal on the same arc)
/_RCB = x (adjacent supplementary angles)
Therefore PBCR is cyclic since angle is equal to opposite external angle /_RCB=/_DPB
Last Q of one of our mx1 papers ;
Two circles intersect at A and B. P is a point on the first circle and Q is a point on the second circle such that PAQ is a straight line. C is a point on the second circle. The tangent to the first circle at P meets QC produced to R.
Prove that PBCR is a cyclic quadrilateral

Construct BA and point D (I forgot to write point Q which is produced from PA and lies on second circle)
let /_DPB = x
/_PAB = x (angle between tangent and chord equal to angle in alternate segment)
/_BAQ = 180 - x (adjacent supplementary angles)
/_BCQ = 180 - x (angles equal on the same arc)
/_RCB = x (adjacent supplementary angles)
Therefore PBCR is cyclic since angle is equal to opposite external angle /_RCB=/_DPB
Attachments
-
11.4 KB Views: 57
Last edited:
Sanical
SpiderAnderson
Re: 2012 HSC MX1 Marathon
New question:

New question:

Re: 2012 HSC MX1 Marathon
Should really justify the 3rd last line being because the exponential function is continuous.2 and e2

Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
ie: arctan (1) = pi/4
EDIT: I'm a sped and typed it wrong way around.
For the record, to indicate inverse tan, we use arctan (x)Yahoo hoo! This one looks fun.
Hmmm...
1/2(ln(x^2+4)) + tan*-1 (x/2) + c (BTW that tan thing is meant to be inverse tan.)

ie: arctan (1) = pi/4
EDIT: I'm a sped and typed it wrong way around.
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Laugh out loud.For the record, to indicate inverse tan, we use arctan (x)
ie: arctan (pi/4) = 1
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Oh dear this is what 2 hours of sleep gets you.
I meant arctan (1) = pi/4
Oh dear me.
wait wtf, did I just say that arctan (pi/4) = 1?Laugh out loud.
Oh dear this is what 2 hours of sleep gets you.
I meant arctan (1) = pi/4
Oh dear me.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX1 Marathon

Find the shortest distance between the two branches of the curve y=(x^2+1) / (x+1)

Find the shortest distance between the two branches of the curve y=(x^2+1) / (x+1)
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX1 Marathon
Clearly someone needs sugar or sleep.wait wtf, did I just say that arctan (pi/4) = 1?
Oh dear this is what 2 hours of sleep gets you.
I meant arctan (1) = pi/4
Oh dear me.
- Joined
- Feb 16, 2005
- Messages
- 8,499
- Gender
- Male
- HSC
- 2006
Re: 2012 HSC MX1 Marathon

This only works if n is an integer. In this case, n is allowed to be any real number. Most people would fall for this trap...
Last edited: