Re: 2012 HSC MX2 Marathon
Might as well bring this back to life.
Prove that the polynomial
=\sum_{k=0}^{2n} \frac{x^k}{k!})
has no real roots. (Where n is a non-negative integer.)
Let's see if this works...
 = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^{2n}}{2n!} )
We know that n is an integer, so 2n must be even. Therefore, p(x) is an even polynomial, as it has a degree of 2n.
From the fundamental theorem of algebra, we also know that there are 2n roots of p(x), therefore we have an even number of roots.
Now the product of all roots (which I am going to call:
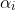
) is
^{2n} \frac{a_{2n}}{a} )
Where a and a_2n are the coefficients of the first and last term respectively (I flipped p(x) around so the x^2n/2n! is the first term)
We know that the a_2n/a must't have a negative 1 out the front, because p(x) is even. For example, look at a quadratic or quartic. The product of roots being c/a and e/a respectively.
Subbing in values for a and a_2n:
 \times\frac{1}{\frac{1}{2n!}} = 2n! )
Now if we take a look at the sum of roots taken 2n-1 at a time (i.e. the product divided by a single root) we find that:

As a_2n = a_(2n-1) = 1.
Now, if we take a closer look at the above sum, we find it can be expressed as:

Cancelling the 2n!, we get

now:

In order for this statement to be true,
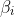
must be complex.
i.e.

This means that
^2 = c^2 - d^2 + 2icd )
In order for
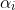
to be complex, both c and d =! 0.
d =! 0 is obvious, as
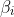
would not be complex if d = 0.
Now, we must show that c =! 0
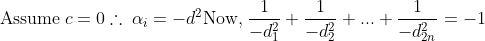
(Where each d_i belongs to its respective
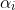
)
Cancelling the negative sign,

Although this looks plausible, d^2 > 1 for it to hold true.
i.e. d < -1 & d > 1 , but d is still not equal to 0
Now, as

We can substitute this back into the original sum.
 &= \sum_{k=0}^2n \frac{(-d_i^2)^k}{k!} \\ &= 1 -d_i^2 + \frac{-d_i^4}{2!} + \frac{-d_i^6}{3!} + ... + \frac{-d_i^4n}{2n!} \end{align*} \\ \therefore \: d_i^2 + \frac{d_i^4}{2} + \frac{d_i^6}{6} + ... + \frac{d_i^4n}{2n!} = 1 )
Now, in order for this expression to hold true, d^2 < 1 or -1< d<1.
However, we already know that d^2 > 1. This leads us to a contradiction; how can d^2 be both less than and greater than 1? This means that our initial assumption, c = 0 is false.
As c, d =! 0, This means that
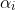
is complex.
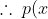 )
has no real roots.
.
.
.
.
.
.
This goddamn better be right, I spent all night on this...
EDIT: Hang on, I don't think I can sub in d^2 into p(x) like that, the even powers will cancel the negative sign
