Since 'n' is even, let
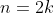
, then we have:
(n+2) = n^3+3n^2+2n=8k^3+12k^2+4k)
Now if this is divisible by 12 like the question claims, then all we have to do is divide by 12 and show that the result is an integer for


Grouping together the fractions gives:
)
Since 'k' is an integer, then
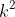
is an integer, and we can disregard it. If we prove the 2nd half is an integer, then the solution is complete, so consider:
)
When 'k 'is a multiple of 3, then it is an integer, so we only have to prove it is an integer for non-multiples of 3.
Consider what
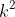
is, it can be expressed as the sum of the odd integers, so multiplying it by two would give:

Now after this we add 1 since it is
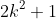
. Notice the difference in the series 2,6,10,14,etc is 4. So the difference is 1 more than a multiple of 3. Since the first term is 2 (one less than a multiple of 3) then we add 1, it becomes a multiple of 3. The next number, since we add 4, also becomes a multiple of 3. This is because:
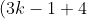 = 3k+3 = 3(k+1))
and hence it also a multiple of 3. Thus in
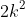
if 'k' is one more than multiple of 3, then next number after it is also a multiple of 3. Hence all that is left to prove is that all integers such that
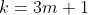
allow
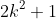
to be divisible by 3.
Now it works for
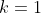
quite trivially. Considering the common difference is 4, adding 4 three times in total adds 12. Now 12 is divisible by 3 and hence all integers of 'k' such that
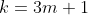
must allow
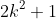
to be divisible by 3. Which concludes the proof.
^2-2(xy+yz+xz) =1-2(xy+yz+xz) \geq 1-2(x^2+y^2+z^2) \Rightarrow x^2+y^2+z^2 \geq \frac{1}{3})
^2+(z-x)^2+(y-z)^2 \geq 0)
#

