Lieutenant_21
Member
Re: HSC 2013 4U Marathon
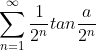
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
So seanieg meant the question is too easy by "troll question" hahaIt's MX1.
Great question:
Great solution! There is a little shorter way:Great question:
First lets establish the identity
Take the natural logarithm of both sides, ensuring that cos(x/2^k) is always positive (absolute value), and use logarithm laws
Differentiate both sides
Take r to infinity

IBPPretty sure that integral can't be expressed in terms of elementary functions.
Yes, I know arctan and cos are elementary functions but you need poly-logarithm functions to do it.Arctan and cos are both elementary functions themselves lol. I still don't think it can be done though.
Yeah I know, I was just responding to you saying you think arctan(cos x) can't be expressed in terms of elementary functions.Yes, I know arctan and cos are elementary functions but you need poly-logarithm functions to do it.
Should have said integral of arctan(cosx)Yeah I know, I was just responding to you saying you think arctan(cos x) can't be expressed in terms of elementary functions.
Anyway, all good.
Could you please elaborate on that?From the early 70s. Those problems are often doable by good mx2 students with no prior olympiad training and this one is no exception.
Thank you!Solve problems haha. And you can find sort of unofficial IMO syllabi various places online to get an idea of useful pieces of theory that are still considered to be at a high school level. (As opposed to advanced university uses of calculus, which are not tested as calculus is not taught properly in high school.)
The point is more to answer things very rigorously with elementary methods. There are many books/articles on problem solving strategies out there, but honestly practicing and reviewing your though processes is probably the most beneficial "training".
Is this not directly quoted from cambridge?Assume it is rational, socan be expressed as a fraction where the numerator and denominator have no common factors:
So now we know thatis even and hence
is even. So now we let
:
So now we know thatis even, and so
is even.
However if bothand
are even, then they have a common factor of
. This is a contradiction and so our assumption is wrong, that is,
is not rational - it is irrational.
According to a lady from Dymocks on george street (Is it george street? lol I think so), cambridge 4u is "for students who are really struggling to grasp the concepts of extension 2 maths, and need help at a basic level"I am pretty sure that was the only mark I lost (hopefully, as I haven't gotten the whole paper back yet). The test wan't really that hard, was very similar to questions found in Cambridge.
I never used Cambridge before but I used it to study for this test because my teacher uses it and I think Cambridge and Terry Lee complement each other very well for 4U.
Why do you think so?Is this not directly quoted from cambridge?
iirc ive read those words verbatim out of either cambridge or some other place. I had a flashback of the exact moment I read them haha.Why do you think so?
