HSC 2013 MX2 Marathon (archive) (2 Viewers)

seanieg89 · May 3, 2013

Re: HSC 2013 4U Marathon

After completing Sy123's question on conjugate roots, it is a nice challenge exercise to consider the analogous problem for cube roots:

$If $P(x)$ is a polynomial with rational coefficients and $\alpha+\sqrt[3]{\beta}$ is a root of $P$ for some rational $\alpha$ and some rational $\beta$ that is not the cube of a rational number, formulate and prove an assertion similar to the conjugate root theorem. (ie find another root or several other roots that $P$ must possess).$

Registered User · May 4, 2013

Re: HSC 2013 4U Marathon

$Evaluate$ $\int_{0}^{\infty }\frac{1}{x^{4}+1}dx$

HeroicPandas · May 4, 2013

Re: HSC 2013 4U Marathon

Registered User said:
$Evaluate$ $\int_{0}^{\infty }\frac{1}{x^{4}+1}dx$

Let integral be I
let x^2 = tanθ

2x.dx = sec^2 θ .dθ

When x= 0, θ = 0
When x = INFTY, θ = pi/2

therefore, int(θ=0 to θ=pi/2) = 0.5 dθ

therefore, I = pi/4?

Sy123 · May 4, 2013

Re: HSC 2013 4U Marathon

HeroicPandas said:
Let integral be I
let x^2 = tanθ

2x.dx = sec^2 θ .dθ

When x= 0, θ = 0
When x = INFTY, θ = pi/2

therefore, int(θ=0 to θ=pi/2) = 0.5 dθ

therefore, I = pi/4?

You have made a mistake when subbing dx back into the integral

Registered User · May 4, 2013

Re: HSC 2013 4U Marathon

HeroicPandas said:
Let integral be I
let x^2 = tanθ

2x.dx = sec^2 θ .dθ

When x= 0, θ = 0
When x = INFTY, θ = pi/2

therefore, int(θ=0 to θ=pi/2) = 0.5 dθ

therefore, I = pi/4?

You can't use that substitution because you can't get rid off the x after you sub dx back.
The only substitution you can use is x=tanx; $\int_{0}^{\infty }\frac{sec^{2}\theta }{tan^{4}\theta+1}d\theta$ which doesn't really help.

Registered User · May 4, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$The polynomial$ \ \ P(x) \ \ $has integer co-efficients$

$p+\sqrt{q} \ \ $is a root of the polynomial, where$ \ \ p, q\ \ $are rational$$

$Prove that$ \ \ p-\sqrt{q} \ \ $must also be a root of the polynomial$

This can be so easily done using abstract algebra but I don't think that is HSC level.

asianese · May 4, 2013

Re: HSC 2013 4U Marathon

Hint: fugly completion of squares

Registered User · May 4, 2013

Re: HSC 2013 4U Marathon

asianese said:
Hint: fugly completion of squares

The final result is nice though. Allows you to evaluate a sine Fresnel Integral without using complex analysis (you need Gamma function though).

Sy123 · May 4, 2013

Re: HSC 2013 4U Marathon

Registered User said:
$Evaluate$ $\int_{0}^{\infty }\frac{1}{x^{4}+1}dx$

Finding roots of unity then expressing in quadratic factors then applying partial fractions, then manipulating to get it into a suitable integral form:

$\frac{1}{x^4+1} = \frac{1}{4\sqrt{2}}\left( \frac{2x+\sqrt{2}}{x^2+\sqrt{2}x+1} - \frac{2x-\sqrt{2}}{x^2-\sqrt{2}x+1}+\frac{\sqrt{2}}{x^2+\sqrt{2}+1} + \frac{\sqrt{2}}{x^2-\sqrt{2}x+1} \right)$

By integrating both sides, we yield:

First and second fractions are logarithms, both elements inside the logarithm functions are monic quadratics, at infinity they cancel to 1, making the first 2 terms together 0, at x=0, the same happens and we get the logarithm of 1 which is again zero.
The second 2 terms are in the form for the atan function. After completing the square and manipulations, we evaluate them at infinity keeping in mind that at infinity atan is pi/2.

In the end we should arrive at

$\frac{\pi}{2\sqrt{2}}$

Also it would be awesome if people started posting these integrals in the integration marathon please =)

Registered User · May 4, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
Finding roots of unity then expressing in quadratic factors then applying partial fractions, then manipulating to get it into a suitable integral form:

$\frac{1}{x^4+1} = \frac{1}{4\sqrt{2}}\left( \frac{2x+\sqrt{2}}{x^2+\sqrt{2}x+1} - \frac{2x-\sqrt{2}}{x^2-\sqrt{2}x+1}+\frac{\sqrt{2}}{x^2+\sqrt{2}+1} + \frac{\sqrt{2}}{x^2-\sqrt{2}x+1} \right)$

By integrating both sides, we yield:

First and second fractions are logarithms, both elements inside the logarithm functions are monic quadratics, at infinity they cancel to 1, making the first 2 terms together 0, at x=0, the same happens and we get the logarithm of 1 which is again zero.
The second 2 terms are in the form for the atan function. After completing the square and manipulations, we evaluate them at infinity keeping in mind that at infinity atan is pi/2.

In the end we should arrive at

$\frac{\pi}{2\sqrt{2}}$

Also it would be awesome if people started posting these integrals in the integration marathon please =)

Good job!

By the way, $\int_{0}^{\infty }sin(x^{2})dx=\frac{1}{\sqrt{\pi }}\int_{0}^{\infty }\frac{1}{x^{4}+1}dx=\frac{\sqrt{\pi} }{2\sqrt{2}}$

No problem, I will post there next time.

HeroicPandas · May 4, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
You have made a mistake when subbing dx back into the integral

ahh yes lol, thanks

Registered User said:
You can't use that substitution because you can't get rid off the x after you sub dx back.
The only substitution you can use is x=tanx; $\int_{0}^{\infty }\frac{sec^{2}\theta }{tan^{4}\theta+1}d\theta$ which doesn't really help.

ah yes i see thanks

Sy123 · May 4, 2013

Re: HSC 2013 4U Marathon

Even though its integration I think it should be asked here because its not really a 'Q1 style' integral.

=============

$In the following question, you may assume the results$

$\int_0^{\infty} f(x) \ dx = \lim_{\alpha \to \infty} \int_0^{\alpha} f(x) \ dx$

$\lim_{j \to \infty} j^n e^{-j}= 0 \ \ \ $for any n$$

$\int_0^{\infty} e^{-x^2} = \frac{\sqrt{\pi}}{2}$

$The integrals$ \ \ I_n \ \ $and$ \ \ J_n \ \ $are defined such that$

$I_n = \int_0^{\infty} x^{2n+1}e^{-x^2} \ dx$

$J_n = \int_0^{\infty} x^{2n}e^{-x^2} \ dx$

$Prove that$

$\frac{J_n}{I_n\sqrt{\pi}} \ \ \ $gives the probability that$ \ \ n \ \ $heads are tossed$$

$on a fair coin which is tossed$ \ \ 2n \ \ $times$

seanieg89 · May 4, 2013

Re: HSC 2013 4U Marathon

Registered User said:
This can be so easily done using abstract algebra but I don't think that is HSC level.

No heavy machinery required here, the simplest proof of this fact that I can think of is essentially identical to the standard proof of a course theorem.

Sy123 · May 5, 2013

Re: HSC 2013 4U Marathon

$Prove that$

$\sum_{r=0}^{n} \frac{(-1)^{r}}{m+r+1} \binom{n}{r} = \frac{m! n!}{(m+n+1)!}$

(there is a reason I asked this in this 4U thread)

RealiseNothing · May 5, 2013

Re: HSC 2013 4U Marathon

In this question you may assume that:

$cos(x) = \sum_0^{\infty} (-1)^k \frac{x^{2k}}{(2k)!}$

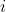$i) Explain why the polynomial$

$P(x) = \frac{(x-a)(x-b)(x-c)(x-d)}{abcd}$

$$has roots a,b,c,d and$~P(0)=1$

$ii) Show that$

$P(x) = (1-\frac{x}{a})(1-\frac{x}{b})(1-\frac{x}{c})(1-\frac{x}{d})$

$iii) Assuming the result in part (ii) holds for polynomials of infinite degree, prove that$

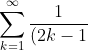$\sum_{k=1}^{\infty} \frac{1}{(2k-1)^2} = \frac{\pi^2}{8}$

seanieg89 · May 5, 2013

Re: HSC 2013 4U Marathon

Lol rather large assumptions there Realise.

RealiseNothing · May 5, 2013

Re: HSC 2013 4U Marathon

seanieg89 said:
Lol rather large assumptions there Realise.

I know haha, but proving those assumptions is a little beyond MX2, so I let people assume it.

RealiseNothing · May 5, 2013

Re: HSC 2013 4U Marathon

seanieg89 said:
Lol rather large assumptions there Realise.

Plus Euler assumed them, why can't we

seanieg89 · May 5, 2013

Re: HSC 2013 4U Marathon

He eventually found a rigorous proof. You actually need quite a lot of machinery to make that particular proof work (much more than you have stated I am pretty sure).

Edit: To be a little more concrete in my criticism, my main objection is that it is not at all clear that the symmetric polynomials in the roots of a power series have to be related to the coefficients of the power series in the same way that is true of polynomials. (In fact this is not true in general.)

To make this argument work we need to assume something along the lines of the Weierstrass factorisation theorem, as well as some facts about convergence and uniform convergence. In short, I think that this isn't a good choice for an MX2 question because I think it is better for the assumptions to be milder and more precise. That way, the student is at least engaging in (close-to) rigorous mathematical reasoning just skipping the theory leading up to the assumption rather than doing a whole series of hand-wavy steps.

Registered User · May 6, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$The polynomial$ \ \ P(x) \ \ $has integer co-efficients$

$p+\sqrt{q} \ \ $is a root of the polynomial, where$ \ \ p, q\ \ $are rational$$

$Prove that$ \ \ p-\sqrt{q} \ \ $must also be a root of the polynomial$

Do you do this questions using the conjugate root theorem?

HSC 2013 MX2 Marathon (archive) (2 Viewers)

Well-Known Member

Member

Heroic!

This too shall pass

Member

Member

Σ

Member

This too shall pass

Member

Heroic!

This too shall pass

Well-Known Member

This too shall pass

what is that?It is Cowpea

Well-Known Member

what is that?It is Cowpea

what is that?It is Cowpea

Well-Known Member

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 2)