Re: HSC 2013 4U Marathon
Yep those are the only solutions, what was your method?
My aim was to construct a cubic polynomial which has roots x, y, z, using sum of roots/product of roots/two at a time. Then by finding the roots of this polynomial, we find the values of x, y, z, that satisfy the system of equations. The cubic is in the form:
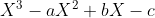
The sum of roots is easy as it's already given:
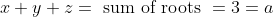
So we have:
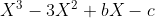
Now we get the value of 'b' by finding the sum of the pair roots (xy+xz+yz). We know that:
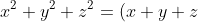^2 - 2(xy+xz+yz))
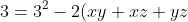)
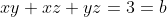
So we now have:

Now we know that x, y, z and the roots of this equation, so by substitution we arrive at:
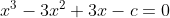
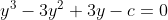
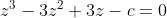
If we add all these together we get:
 - 3(x^2+y^2+z^2) + 3(x+y+z) = 3c)
-3(3)+3(3) = 3c)
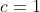
So our polynomial is:
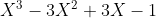
Which simplifies to:
^3 = 0)
Which has all roots equal to 1. So x, y, z are all equal to 1. And the polynomial can not have other roots and so this is the only possible solution set to the given system of equations.
