Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
Take arbitrary rationals with integer variables
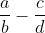
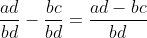
In order to minimize the gap between two arbitrary numbers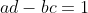
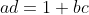
But using the p,q,r notation is easier I think it says the same thing however
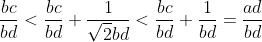
Meaning the middle bound is still rational
The smallest gap yes, I mean that the smallest gap between any 2 rational numbers is 1/(common denominator).By lowest gap I'm assuming you mean smallest gap? I don't thinkis the smallest gap. Consider:
would be the smallest gap between all number of the form
where the denominator is fixed and numerator varies. But the denominator isn't necessarily fixed.
Take arbitrary rationals with integer variables
In order to minimize the gap between two arbitrary numbers
But using the p,q,r notation is easier I think it says the same thing however
Meaning the middle bound is still rational
