Paradoxica
-insert title here-
Re: MX2 2015 Integration Marathon

Anyway, for your question, change the denominator into the square of sine, split the integrand, and use IBP on the term containing the x. The new integral resulting from this cancels out the other term which we did not touch, leaving behind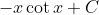
Haha, I think "nuts" is an understatementFinally a question which isn't completely nuts
Although I do quite enjoy reading Ekman's and Paradoxica's solutions to some of their harder integrals, I admit.

Anyway, for your question, change the denominator into the square of sine, split the integrand, and use IBP on the term containing the x. The new integral resulting from this cancels out the other term which we did not touch, leaving behind
Last edited:

