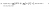if f(x) is my function then f'(x) is my derivative, so subbing c into the derivative, i.e f'(c), will give me a constantYeah I know what the MVT is, but I don't really get how your proof of seanieg89's question actually works (like how do you assume f'(c) is constant, presumably as you range x and y)
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC Mathematics Marathon (1 Viewer)
- Thread starter ohexploitable
- Start date
blackops23
Member
- Joined
- Dec 15, 2010
- Messages
- 428
- Gender
- Male
- HSC
- 2011
Sorry guys someone please explain this to me, how do you know the series is geometric? havent done much work with series :S
Last edited:
Wight
ಠ_ಠ
- Joined
- Mar 11, 2010
- Messages
- 146
- Gender
- Male
- HSC
- 2011
you cannot assume that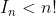
now is a solution like this accepted?
I also do not have another question...someone else can put one up.
idk if you can use induction like that it's like taking the easy way out
now is a solution like this accepted?
I also do not have another question...someone else can put one up.
Last edited:
Some Vunt
Banned
What's the current question?
last part of In oneWhat's the current question?
Wight
ಠ_ಠ
- Joined
- Mar 11, 2010
- Messages
- 146
- Gender
- Male
- HSC
- 2011
as forstart with
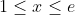
So as any irrational (< 1)^n is even smaller, then as
Yeah the above will need alot more work to suit a proper solution...just a general idea.
I'm still curious as to whether you can use induction...it's obviously the longer process, but the easier way out when you don't think of the obvious...can anyone clarify?
Last edited:
apollo1
Banned
- Joined
- Sep 19, 2011
- Messages
- 938
- Gender
- Male
- HSC
- 2011
can we solve this using hsc knowledge?
you use the series
S = 1+xcisx+(xcisx)^2+....+(xcisx)^n
then sum it using a gp and equate the real parts
for it to conerge |r| if r is the common ratio must be <1
but since r is xcisx then |r| = x
so x<1 for it to converge?
apollo1
Banned
- Joined
- Sep 19, 2011
- Messages
- 938
- Gender
- Male
- HSC
- 2011
can someone help me with this question:
Attachments
-
14.7 KB Views: 54
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 195
- Gender
- Male
- HSC
- 2011
you mean |x| < 1, negative values of x and zero still workyou use the series
S = 1+xcisx+(xcisx)^2+....+(xcisx)^n
then sum it using a gp and equate the real parts
for it to conerge |r| if r is the common ratio must be <1
but since r is xcisx then |r| = x
so x<1 for it to converge?
to make sure the GP converges, do it like this:
So if we let
which converges as n->infinity if |z| < 1, and diverges if |z|>1. If |z|=1, i.e. x = 1 or -1, it neither converges nor diverges: it just sorta oscillates around the place (although, since 1 is not a rational multiple of pi, its not actually periodic but rather slightly chaotic). Clearly |z| = |x|, so it converges iff |x|<1, goes weird if |x| = 1 and diverges if |x| > 1.
Cool question!
EDIT: oh wait I kinda messed it up because I showed the cis sum diverges, not Re(cissum). Its pretty easy to do that though I think:
Now note that as n goes to infinity, the demoninator remains the same while the numerator converges if |x|<1. For |x|>=1, its a lot more complicated but it certainly doesnt converge; it doesnt necessarily "increase without bound though", it sorta oscillates whilst "diverging" at the same time (I dont actually know the technical definition of diverging so yeah, in this case a function like xsinx diverges even though it has zeroes for arbitrarily large x)
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Exactly, and your mention of the chaotic nature of the partial sums for certain x brings up an interesting point...consider the same problem if you replace the series by:you mean |x| < 1, negative values of x and zero still work
to make sure the GP converges, do it like this:
So if we let
which converges as n->infinity if |z| < 1, and diverges if |z|>1. If |z|=1, i.e. x = 1 or -1, it neither converges nor diverges: it just sorta oscillates around the place (although, since 1 is not a rational multiple of pi, its not actually periodic but rather slightly chaotic). Clearly |z| = |x|, so it converges iff |x|<1, goes weird if |x| = 1 and diverges if |x| > 1.
Cool question!
(Considerably harder than the geometric series case)