Thought of a method that should work (and give us a more general formula), but it takes some doing. Will work through the details later today and post them when I do.
Okay, I actually really can't be bothered to write everything up, but I will sketch each step of my computation. (This will evaluate the sum for any pair of odd integers in the numerator. Extending this to treat non-odd integers is not difficult, but it clutters the computations with (-1)^n parity factors.)
(This proof isn't very clean and there could very well be a nicer way of going about things.)
1. By using the products to differences formula, it suffices to figure out how to calculate things of the form
}{1+\cos(k\pi/100)}\quad \textrm{for }m\in\mathbb{Z}.)
2. Now a couple of trig identities, together with De'Moivres and the geometric series formula allow us to deduce the recurrence relation

3. This is just a simple inhomogenous difference equation, In fact the LHS of the above is just a second order difference about m, which motivates the solution being quadratic. Indeed, all solutions are of the form
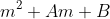
, with A and B undetermined constants. This reduces the problem to computing A and B.
4. This can be done by explicitly computing
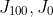
and solving the resulting simultaneous equations. To compute these two intial values of J, we have to sum 1/(1+cos(k*pi/100)). The summand is equal to 1/(2cos^2(k*pi/200)). We can treat such sums in ways analogous to the calculation in the "rigorous elementary method" section of
https://en.wikipedia.org/wiki/Basel_problem.
Putting this all together completes the computation. I definitely won't write the whole working out, but I will write out my resulting formulae.
