Last edited:
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MATH1081 Discrete Maths (2 Viewers)
- Thread starter leehuan
- Start date
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Discrete Maths Sem 2 2016
I just wasn't sure how to manipulate my x in. And yet again I forgot that you had to prove they are a mutual subset of each other to be equal sets.
Sounds right. Jim Franklin seems to prefer to drill us into using slightly more formalised proofs though.if i remember its easier to prove by Venn Diagrams
I just wasn't sure how to manipulate my x in. And yet again I forgot that you had to prove they are a mutual subset of each other to be equal sets.
RenegadeMx
Kosovo is Serbian
- Joined
- May 6, 2014
- Messages
- 1,301
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2016
Re: Discrete Maths Sem 2 2016
havent heard of him before, but had a look at your course outline you lucky fucks will have peter brownSounds right. Jim Franklin seems to prefer to drill us into using slightly more formalised proofs though.
I just wasn't sure how to manipulate my x in. And yet again I forgot that you had to prove they are a mutual subset of each other to be equal sets.
Re: Discrete Maths Sem 2 2016
$ iff $T \subseteq S$. Also for any set $S$, $S$ is in its power set.$)
 = P(B)$. Since $A \in P(A)$, we have $A \in P(B)$ (as $P(A)=P(B)$), so $A\subseteq B$. Reversing the roles of $A$ and $B$ shows $B\subseteq A$. So $A=B$.$)
I can see why it is but how would you prove it
Re: Discrete Maths Sem 2 2016
To show A is a subset of B, you should start off by letting x be an element of A (you did A∩C), and then show it is an element of B. (You may want to consider cases along the way to help use the given info.)
I think what you essentially did is show A∩C is a subset of B.
To show A is a subset of B, you should start off by letting x be an element of A (you did A∩C), and then show it is an element of B. (You may want to consider cases along the way to help use the given info.)
I think what you essentially did is show A∩C is a subset of B.
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Discrete Maths Sem 2 2016
___________________________
The answers don't even tell me if it's true or false so I assumed it was true (because I could not find any counterexample) but then I got stuck proving the latter part.
=(A\times B)\cup (A\times C))
Basically I got stuck proving the RHS is a subset of the LHS
Nice that makes sense. I'm just used to element wise because the lecturers said so lol.Another way of doing it that doesn't involve taking elements is:
Where thestep follows from applying the question assumptions to replace
with the supersets
respectively.
___________________________
The answers don't even tell me if it's true or false so I assumed it was true (because I could not find any counterexample) but then I got stuck proving the latter part.
Basically I got stuck proving the RHS is a subset of the LHS
Last edited:
Re: Discrete Maths Sem 2 2016
Note the RHS is a set of ordered pairs. Let (x,y) be an element of RHS.
Then (x,y) is in A x B or in A x C.
If it's in A x B, then x is in A and y is in B ==> x is in A and y is in B union C. (As B is a subset of B union C.)
The other case you can similarly show that x is in A and y is in B union C.
So in either case, (x,y) is in A x (B union C).
So RHS is a subset of LHS.
A way to show RHS is a subset of LHS.Nice that makes sense. I'm just used to element wise because the lecturers said so lol.
___________________________
The answers don't even tell me if it's true or false so I assumed it was true (because I could not find any counterexample) but then I got stuck proving the latter part.
Basically I got stuck proving the RHS is a subset of the LHS
Note the RHS is a set of ordered pairs. Let (x,y) be an element of RHS.
Then (x,y) is in A x B or in A x C.
If it's in A x B, then x is in A and y is in B ==> x is in A and y is in B union C. (As B is a subset of B union C.)
The other case you can similarly show that x is in A and y is in B union C.
So in either case, (x,y) is in A x (B union C).
So RHS is a subset of LHS.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Discrete Maths Sem 2 2016
Have you learned that the symmetric difference is associative? If not, then prove this as an exercise as it is easy and has this claim is a trivial consequence.
Indeed, We have A*C=B*C => (A*C)*C=(B*C)*C => A*(C*C)=B*(C*C) => A*e=B*e => A=B where e denotes the empty set and * denotes the symmetric difference operation.
(In fact we are proving a property of abstract groups here. An algebra of sets endowed with the symmetric difference is an abelian group.)
Have you learned that the symmetric difference is associative? If not, then prove this as an exercise as it is easy and has this claim is a trivial consequence.
Indeed, We have A*C=B*C => (A*C)*C=(B*C)*C => A*(C*C)=B*(C*C) => A*e=B*e => A=B where e denotes the empty set and * denotes the symmetric difference operation.
(In fact we are proving a property of abstract groups here. An algebra of sets endowed with the symmetric difference is an abelian group.)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Discrete Maths Sem 2 2016
I will work on it later. It doesn't look hard if I give it a bit of thought.
We weren't actually taught what symmetric difference is really. It's just a homework question regarding it.
I will work on it later. It doesn't look hard if I give it a bit of thought.
We weren't actually taught what symmetric difference is really. It's just a homework question regarding it.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Discrete Maths Sem 2 2016
I think I'm forgetting something.
I understand how a function f is surjective iff the codomain of f is the range. However what's the problem if the codomain was a proper subset of f?
Also, are these supposed to be two notations for the same thing
=x^3\qquad f:x \mapsto x^3)
I think I'm forgetting something.
I understand how a function f is surjective iff the codomain of f is the range. However what's the problem if the codomain was a proper subset of f?
Also, are these supposed to be two notations for the same thing
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Discrete Maths Sem 2 2016
Alright cool.
My bad on the first qn, meant a subset of the range. So something like
, \, f(x)=x^3)
Edit: Oh crap, is it because when x=-1 (which is in R), there is no output value?
With that maps-to notation though I have another question. How would you write something like f:R->R, f(x)=x?
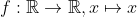
Alright cool.
My bad on the first qn, meant a subset of the range. So something like
Edit: Oh crap, is it because when x=-1 (which is in R), there is no output value?
With that maps-to notation though I have another question. How would you write something like f:R->R, f(x)=x?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: Discrete Maths Sem 2 2016
That doesn't make any sense, when you talk about a function, you have to specify a domain and a codomain for that function. Loosely speaking a function is a pair of sets X,Y and a rule that assigns to every element of X an element of Y.
The range is the set of elements of Y that are actually hit, ie the range is always a subset of the codomain.
That doesn't make any sense, when you talk about a function, you have to specify a domain and a codomain for that function. Loosely speaking a function is a pair of sets X,Y and a rule that assigns to every element of X an element of Y.
The range is the set of elements of Y that are actually hit, ie the range is always a subset of the codomain.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Discrete Maths Sem 2 2016
Wait what? Now I'm confused.
I resolved my question mainly based off something like this:
=\frac{1}{x}\\ \text{is not a function (despite what bull high school says) because when }x=0\text{ there is no defined value for }f(0))
I was wondering why something like this 'function' is not surjective:
, f(x)=x^3)
But then I realised that it's not a function because when x<0, there are no output values.
(Edit: Or maybe I do actually. I think I might've abused the term "range")
Wait what? Now I'm confused.
I resolved my question mainly based off something like this:
I was wondering why something like this 'function' is not surjective:
But then I realised that it's not a function because when x<0, there are no output values.
(Edit: Or maybe I do actually. I think I might've abused the term "range")
