leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: MATH2601 Linear Algebra/Group Theory Questions
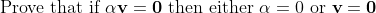
I have most of the proof covered up but I'm getting confused at the last bit.
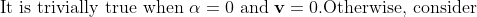
\textbf{v}=0\textbf{v}=\textbf{0}&=-\alpha\textbf{v}\\ \therefore \alpha\textbf{v}&=-\alpha\textbf{v}\end{align*})
&= \alpha^{-1}(-\alpha\textbf{v})\\ \textbf{v}&=-\textbf{v}\\ 2\textbf{v}&=0\\ \textbf{v}&=0\end{align*})
All I'm really stuck on is how to prove that if v \neq 0 why must alpha be equal to 0
I have most of the proof covered up but I'm getting confused at the last bit.
All I'm really stuck on is how to prove that if v \neq 0 why must alpha be equal to 0

