-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MATH2621 Higher Complex Analysis (1 Viewer)
- Thread starter leehuan
- Start date
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
This isn't actually a question I got from the course but I'm not sure if it can be done via 4U techniques so I decided to leave it here. I know intuitively why it works but I'm curious as to the proper proof of it
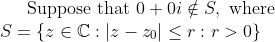
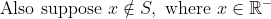
\text{ is obtained when }z\text{ lies on the boundary }\partial S\\ \text{and additionally prove that the corresponding value of }z\text{ chosen must be such that}\\ \text{a ray drawn from }0+0i\text{ to }z\text{ is tangential to the disk at }z)
Feel free to change this question into an R2 question if that makes it easier. If the proof happens to be long just a description will be plenty.
(I actually don't know if this question is correct or not. It was a deduction I made based off a few CSSA papers.)
Feel free to change this question into an R2 question if that makes it easier. If the proof happens to be long just a description will be plenty.
(I actually don't know if this question is correct or not. It was a deduction I made based off a few CSSA papers.)
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
By invariance of the properties in question under rotation and dilation about the origin it suffices to consider disks of radius r < 1 centred at z0=1.
Then for any fixed angle w in (-pi,pi], we can consider the ray z=t*cis(w). Finding the distance of this ray from z0 is optimising a single variable quadratic (or remembering a formula). This ray has nonempy intersection with the disk iff this distance does not exceed r. This gives us an interval of w (|sin(w)| =< r) for which the ray meets the disk, so we can then consider the endpoints of this interval.
Then for these optimal w, the quadratic equation in x coming from y=tan(w)x and (x-1)^2+y^2=r^2 is easily shown to have 0 discriminant. i.e. the rays with optimal argument meet the disks tangentially.
Then for any fixed angle w in (-pi,pi], we can consider the ray z=t*cis(w). Finding the distance of this ray from z0 is optimising a single variable quadratic (or remembering a formula). This ray has nonempy intersection with the disk iff this distance does not exceed r. This gives us an interval of w (|sin(w)| =< r) for which the ray meets the disk, so we can then consider the endpoints of this interval.
Then for these optimal w, the quadratic equation in x coming from y=tan(w)x and (x-1)^2+y^2=r^2 is easily shown to have 0 discriminant. i.e. the rays with optimal argument meet the disks tangentially.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
The last two terms vary in meaning between different authors etc. One of them could very well have a nonempty requirement in your course ("region" sometimes has this in particular, "domains" are a little more standard and usually just refer to open connected subsets of C in this context.)
4025808
Well-Known Member
I remember doing a taylor series on that one, where e^z = 1 +z + z^2 /2 + z^3/3! + ...
I can't assume anything about complex differentiability yet
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
At the time I wanted to avoid it because of the fact we hadn't done differentiation but turns out it was the next lecture lol. So I ended up just L'H smashing it.I remember doing a taylor series on that one, where e^z = 1 +z + z^2 /2 + z^3/3! + ...
Which is probably me cheating, because this is the definition of the derivative, but I'm in C so I'll cheat by using the Cauchy-Riemann equations instead
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
How does that make it any less cheating?At the time I wanted to avoid it because of the fact we hadn't done differentiation but turns out it was the next lecture lol. So I ended up just L'H smashing it.
Which is probably me cheating, because this is the definition of the derivative, but I'm in C so I'll cheat by using the Cauchy-Riemann equations instead
You should use the definition of the exponential explicitly (presumably it is the power series centred at 0, so the argument is much the same). Don't assume anything about the differentiability of the exponential if the limit you are asked to evaluate (if it exists) is the definition of the derivative.
Same with L'Hopital. Eg you could try to find the limit of sin(x)/x as x tends to zero by using L'Hopital and it "works" in that cos(x)/1 clearly does tend to 1. However how did we prove that sin(x) has derivative cos(x)? It turns out we need to essentially evaluate the limit of sin(x)/x in order to do this!
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
That being said,How does that make it any less cheating?
You should use the definition of the exponential explicitly (presumably it is the power series centred at 0, so the argument is much the same). Don't assume anything about the differentiability of the exponential if the limit you are asked to evaluate (if it exists) is the definition of the derivative.
Same with L'Hopital. Eg you could try to find the limit of sin(x)/x as x tends to zero by using L'Hopital and it "works" in that cos(x)/1 clearly does tend to 1. However how did we prove that sin(x) has derivative cos(x)? It turns out we need to essentially evaluate the limit of sin(x)/x in order to do this!
When you first told me that the power series was the definition of the exponential I initially accepted it, but became reluctant to believe. Why is that the case? Or do they just teach things in the wrong order?
Because the power series falls out of differentiation as well.
I get your point, but I really don't know how I feel about the power series definition. I would've thought that the limit definition
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Because working with power series is pretty low level analysis, you don't need much theory development before you can start saying meaningful things about functions defined via power series. (Eg it is smooth and invariant under differentiation, which almost uniquely characterises the exponential.)That being said,
When you first told me that the power series was the definition of the exponential I initially accepted it, but became reluctant to believe. Why is that the case? Or do they just teach things in the wrong order?
Because the power series falls out of differentiation as well.
I get your point, but I really don't know how I feel about the power series definition. I would've thought that the limit definitionwas more acceptable. (Hopefully I got that right because I didn't double check)
Same with trig functions. From power series definitions we can recover all of the familiar properties of these guys. This is more for efficient structuring of theory rather than mirroring historical progression (logs came first!) or being the best way to learn what a trig/exp function is (high school does a decent job here).
It is easy to show that your expression and the power series defn are equivalent, so it is a matter of choice. Again, power series are usually very pleasant to work with if we are doing calculus and thus preferable.
