You should really sayProve that: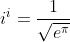
By definition,
If you didn't use pv then you'd get something like a + exp(2pi k) term as well... (The complex exponential function is periodic)
EDIT: Just saw the posted solutions... You should really use pv (principal value) for the fore mentioned reasons. But this is all complex analysis (usually a second year university course).
Last edited:


